题目内容
已知函数 R).
R).
(1)若曲线 在点
在点 处的切线与直线
处的切线与直线 平行,求
平行,求 的值;
的值;
(2)在(1)条件下,求函数 的单调区间和极值;
的单调区间和极值;
(3)当 ,且
,且 时,证明:
时,证明:
 R).
R).(1)若曲线
 在点
在点 处的切线与直线
处的切线与直线 平行,求
平行,求 的值;
的值;(2)在(1)条件下,求函数
 的单调区间和极值;
的单调区间和极值;(3)当
 ,且
,且 时,证明:
时,证明:
(1)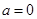 ;(2)详见解析.
;(2)详见解析.
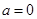 ;(2)详见解析.
;(2)详见解析. 试题分析:(1)欲求a的值,根据在点(1,f(1))处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率.再列出一个等式,最后解方程组即可得.
(2)先求出f(x)的导数,根据f′(x)>0求得的区间是单调增区间,f′(x)<0求得的区间是单调减区间,最后求出极值即可.
(3)由(2)知,当a=1时,函数f(x)=
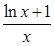 ,在[1,+∞)上是单调减函数,且f(1)=
,在[1,+∞)上是单调减函数,且f(1)=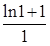 =1,从而证得结论..
=1,从而证得结论..试题解析:解:(1)函数

所以
 又曲线
又曲线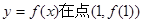 处的切线与直线
处的切线与直线 平行,所以
平行,所以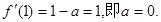 4分;
4分;(2)令
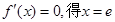
当x变化时,
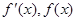 的变化情况如下表:
的变化情况如下表: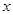 | 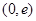 | 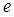 | 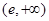 |
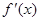 | + | 0 | — |
 |  | 极大值 |  |
 的单调递增区间是
的单调递增区间是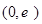 ,单调递减区间是
,单调递减区间是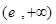
所以
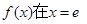 处取得极大值,
处取得极大值,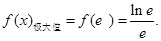 8分;
8分;(3)当
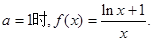 由于
由于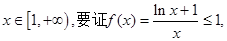
只需证明
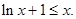
令
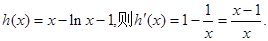
因为
 ,所以
,所以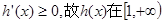 上单调递增,
上单调递增,当
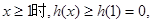 即
即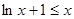 成立。
成立。故当
 时,有
时,有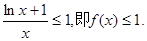 12分;
12分;
练习册系列答案
相关题目
 .
. R),使得f(x)≥kx十b且g(x)≤kx+b对一切x>0恒成立?若存在,求出该一次函数的表达式;若不存在,请说明理由.
R),使得f(x)≥kx十b且g(x)≤kx+b对一切x>0恒成立?若存在,求出该一次函数的表达式;若不存在,请说明理由. ,且
,且 .
. 的值;
的值; 的单调区间;
的单调区间; ,若函数
,若函数 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围. .
. 的单调性,并说明理由;
的单调性,并说明理由; 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,3)内的图像如图所示.记y=f(x)的导函数为y=f¢(x),则不等式f¢(x)≤0的解集为( )
,3)内的图像如图所示.记y=f(x)的导函数为y=f¢(x),则不等式f¢(x)≤0的解集为( )
 ,1]∪[2,3)
,1]∪[2,3) ]∪[
]∪[ ,
, ]
] 有两个极值点
有两个极值点 ,且
,且 ,
, ,则( )
,则( )



 ,函数
,函数 ,若
,若 在
在 上是单调减函数,则
上是单调减函数,则 的取值范围是
的取值范围是


