题目内容
已知平面上直线l的方向向量 ,点O(0,0)和P(-2,2)在直线l的正射影分别是O'和P',且
,点O(0,0)和P(-2,2)在直线l的正射影分别是O'和P',且 ,则λ等于
,则λ等于
- A.

- B.

- C.

- D.

C
分析:观察出向量 是一个单位向量,做出向量
是一个单位向量,做出向量 在单位向量上的投影,比较两个向量的模长之间的关系,即确定了系数的绝对值,再根据两个向量之间的夹角是钝角,确定系数的符号.
在单位向量上的投影,比较两个向量的模长之间的关系,即确定了系数的绝对值,再根据两个向量之间的夹角是钝角,确定系数的符号.
解答:∵ ,
,
直线l的方向向量 ,
,
∴ 在
在 上的投影是-2×
上的投影是-2× ,
,
∵ 是一个单位向量,两个向量的夹角是钝角,
是一个单位向量,两个向量的夹角是钝角,
∴当 时,
时, ,
,
故选C.
点评:本题考查平面向量数量积的含义与物理意义,考查一个向量在另一个向量上的投影,解决本题最关键的是看清两个向量之间的夹角是钝角,从而确定系数的符号.
分析:观察出向量
 是一个单位向量,做出向量
是一个单位向量,做出向量 在单位向量上的投影,比较两个向量的模长之间的关系,即确定了系数的绝对值,再根据两个向量之间的夹角是钝角,确定系数的符号.
在单位向量上的投影,比较两个向量的模长之间的关系,即确定了系数的绝对值,再根据两个向量之间的夹角是钝角,确定系数的符号.解答:∵
 ,
,直线l的方向向量
 ,
,∴
 在
在 上的投影是-2×
上的投影是-2× ,
,∵
 是一个单位向量,两个向量的夹角是钝角,
是一个单位向量,两个向量的夹角是钝角,∴当
 时,
时, ,
,故选C.
点评:本题考查平面向量数量积的含义与物理意义,考查一个向量在另一个向量上的投影,解决本题最关键的是看清两个向量之间的夹角是钝角,从而确定系数的符号.

练习册系列答案
相关题目
 的最小值为
的最小值为 选做题
选做题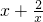 ,判断f(x)在(0,
,判断f(x)在(0, )上的单调性并加以证明;
)上的单调性并加以证明; 与直线
与直线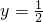 相交,若在y轴右侧的交点自左向右依次记为M1,M2,M3,…,则
相交,若在y轴右侧的交点自左向右依次记为M1,M2,M3,…,则 等于
等于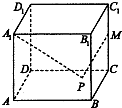 如图,正方体ABCD-A1B1C1D1中,M为CC1的中点,P为平面ABCD内的动点,且A1P和MP与平面ABCD所成的角相等,则P的轨迹为________.
如图,正方体ABCD-A1B1C1D1中,M为CC1的中点,P为平面ABCD内的动点,且A1P和MP与平面ABCD所成的角相等,则P的轨迹为________. n(5n-1),(n∈N+,现从前m项:a1,a2,…,an中抽出一项(不是an,也不是am),余下各项的算术平均数为37,则抽出的是
n(5n-1),(n∈N+,现从前m项:a1,a2,…,an中抽出一项(不是an,也不是am),余下各项的算术平均数为37,则抽出的是