题目内容
已知函数f(x)=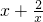 ,判断f(x)在(0,
,判断f(x)在(0, )上的单调性并加以证明;
)上的单调性并加以证明;
解:函数f(x)=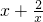 在(0,
在(0, )上是单调减函数,
)上是单调减函数,
下面证明这个判断:
证明:任取x1,x2∈(0, ),且x1<x2
),且x1<x2
f(x1)-f(x2)= -(
-( )=(x1-x2)+(
)=(x1-x2)+( )=
)=
∵<0x1<x2< ,∴x1-x2<0,0<x1x2<2,∴x1x2-2<0,∴
,∴x1-x2<0,0<x1x2<2,∴x1x2-2<0,∴ >0,
>0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2),
∴f(x)在(0, )上是减函数.
)上是减函数.
分析:单调性的证明要充分利用定义,格式步骤是①在单调区间上设x1<x2,②作差f(x1)-f(x2)化简,③判断f(x1)-f(x2)的符号进而判断函数的单调性.
点评:本题考查了函数的单调性的判断,利用单调性的定义证明函数的单调性;对单调性定义的考查是高考以及各类考试的重点,要给予充足的重视.
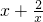 在(0,
在(0, )上是单调减函数,
)上是单调减函数,下面证明这个判断:
证明:任取x1,x2∈(0,
 ),且x1<x2
),且x1<x2f(x1)-f(x2)=
 -(
-( )=(x1-x2)+(
)=(x1-x2)+( )=
)=
∵<0x1<x2<
 ,∴x1-x2<0,0<x1x2<2,∴x1x2-2<0,∴
,∴x1-x2<0,0<x1x2<2,∴x1x2-2<0,∴ >0,
>0,∴f(x1)-f(x2)>0,即f(x1)>f(x2),
∴f(x)在(0,
 )上是减函数.
)上是减函数.分析:单调性的证明要充分利用定义,格式步骤是①在单调区间上设x1<x2,②作差f(x1)-f(x2)化简,③判断f(x1)-f(x2)的符号进而判断函数的单调性.
点评:本题考查了函数的单调性的判断,利用单调性的定义证明函数的单调性;对单调性定义的考查是高考以及各类考试的重点,要给予充足的重视.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|