题目内容
已知函数f(x)=﹣ x3+x2+3x+a.
x3+x2+3x+a.
(1)求f(x)的单调区间;
(2)若f(x)在区间[﹣3,3]上的最小值为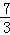 ,求a的值.
,求a的值.
(1)单调减区间为(-∞,-1]和[3,+∞),单调减区间为[-1,3].;(2)a=4.
解析试题分析:(1)首先求出导数,利用导数的为正,为负,可得函数的单调增(减)区间;
(2)先用a的代数式表示出f(x)在区间[-3,3]上的最小值,由已知建立出关于a的方程,解此方程可求a的值.
试题解析:(1)∵f(x)=- x3+x2+3x+a,
x3+x2+3x+a,
∴f′(x)=-x2+2x+3,
令f′(x)>0,得-1<x<3;令f′(x)<0,得x<-1或x>3,
∴所求f(x)的单调减区间为(-∞,-1]和[3,+∞),单调减区间为[-1,3].
(2)当x∈[-3,-1]时,f′(x)<0,[-1,3]时,f′(x)>0
∴f(x)≥f(-1). +1-3+a=
+1-3+a=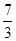 ,∴a=4.
,∴a=4.
考点:1.函数的单调性;2函数的最值.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
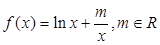 .
.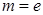 (
(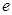 为自然对数的底数)时,求
为自然对数的底数)时,求 的最小值;
的最小值;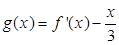 零点的个数;
零点的个数;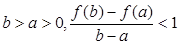 恒成立,求
恒成立,求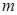 的取值范围.
的取值范围.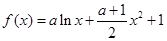 .
.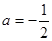 时,求
时,求 在区间
在区间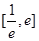 上的最值;
上的最值;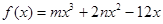 的减区间是(-2,2)
的减区间是(-2,2)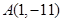 且与曲线
且与曲线 相切的切线方程;
相切的切线方程;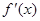 是
是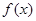 的导函数,
的导函数, ,且函数
,且函数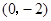 .
.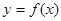 的表达式;
的表达式;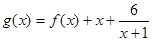 的单调区间和极值.
的单调区间和极值. ,若
,若 。
。 线
线 在点(0,1)处的切线方程为________________
在点(0,1)处的切线方程为________________ 在点(1,-1)处的切线方程是 .
在点(1,-1)处的切线方程是 .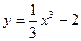 以点(1,-
以点(1,-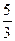 )为切点的切线的倾斜角为
)为切点的切线的倾斜角为