题目内容
已知菱形ABCD中,对角线AC=
,BD=1,P是AD边上的动点,则
•
的最小值为
.
| 3 |
| PB |
| PC |
| 1 |
| 2 |
| 1 |
| 2 |
分析:分别以对角线BD,AC为x轴、y轴建立直角坐标系,设P(x,y),由
∥
可得
y+
-
x=0,代入
•
=(-
-x,-y)•(-x,
-y)=-
x+x2-
y+y2=4x2-4x+
根据二次函数的性质可求
| AP |
| AD |
| 1 |
| 2 |
| ||
| 4 |
| ||
| 2 |
| PB |
| PC |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
解答: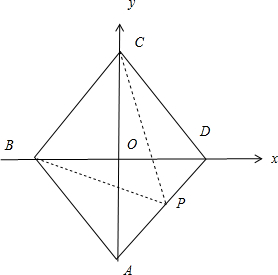 解:分别以对角线BD,AC为x轴、y轴建立如图所示的直角坐标系
解:分别以对角线BD,AC为x轴、y轴建立如图所示的直角坐标系
∵AC=
,BD=1,AC⊥BD
∴A(0,-
),B(-
,0),C(0,
),D(
,0),
=(
,
)
∵P是AD边上的动点,设P(x,y),
=(x,y+
),
∵
∥
∴
y+
-
x=0
∵
=(-x,
-y ),
=(-
-x,-y)
∴
•
=(-
-x,-y)•(-x,
-y)
=-
x+x2-
y+y2=4x2-4x+
根据二次函数的性质可知,当x=
时,值最小为
故答案为:
 解:分别以对角线BD,AC为x轴、y轴建立如图所示的直角坐标系
解:分别以对角线BD,AC为x轴、y轴建立如图所示的直角坐标系∵AC=
| 3 |
∴A(0,-
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| AD |
| 1 |
| 2 |
| ||
| 2 |
∵P是AD边上的动点,设P(x,y),
| AP |
| ||
| 2 |
∵
| AP |
| AD |
∴
| 1 |
| 2 |
| ||
| 4 |
| ||
| 2 |
∵
| PC |
| ||
| 2 |
| PB |
| 1 |
| 2 |
∴
| PB |
| PC |
| 1 |
| 2 |
| ||
| 2 |
=-
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
根据二次函数的性质可知,当x=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题主要考查了向量数量积的坐标表示的应用,二次函数性质的应用,属于基础试题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 (如图1所示),将菱形ABCD沿对角线
(如图1所示),将菱形ABCD沿对角线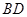 翻折,使点
翻折,使点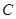 翻折到点
翻折到点 的位置(如图2所示),点E,F,M分别是AB,DC1,BC1的中点.
的位置(如图2所示),点E,F,M分别是AB,DC1,BC1的中点.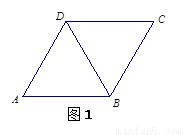

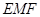 ;
;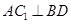
 时,求线段AC1 的长.
时,求线段AC1 的长.