题目内容
7.i是虚数单位,已知$\frac{ai+1}{i}$=bi+1,则a+b为( )| A. | -2 | B. | 0 | C. | 2 | D. | 1-i |
分析 利用复数代数形式的乘除运算化简,再由复数相等的条件求得a,b的值,则答案可求.
解答 解:由$\frac{ai+1}{i}$=$\frac{(1+ai)(-i)}{-{i}^{2}}=a-i$=bi+1,
得a=1,b=-1,
∴a+b=0.
故选:B.
点评 本题考查复数代数形式的乘除运算,考查复数相等的条件,是基础的计算题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知集合M=$\{x|\frac{2-x}{x+1}≥0\}$,N={y|y=lnx},则M∩N=( )
| A. | (0,2] | B. | (-1,2] | C. | (-1,+∞) | D. | R |
18.已知甲、乙、丙三种食物的维生素及成本入戏表实数:
某学校食堂欲将这三种食物混合加工成100kg混合食物,且要求混合食物中至少需要含35000单位的维生素C及40000单位的维生素D.
(1)设所用食物甲、乙、丙的质量分别为xkg,ykg,100-x-ykg(x≥0,y≥0),试列出x,y满足的数学关系式,并画出相应的平面区域;
(2)用x,y表示这100kg混合食物的成本z,求出z的最小值.
| 食物类型 | 甲 | 乙 | 丙 |
| 维生素C(单位/kg) | 300 | 500 | 300 |
| 维生素D(单位/kg) | 700 | 100 | 300 |
| 成本(元/kg) | 5 | 4 | 3 |
(1)设所用食物甲、乙、丙的质量分别为xkg,ykg,100-x-ykg(x≥0,y≥0),试列出x,y满足的数学关系式,并画出相应的平面区域;
(2)用x,y表示这100kg混合食物的成本z,求出z的最小值.
15.函数y=x+lnx2的大致图象为( )
| A. |  | B. |  | ||
| C. |  | D. |  |
17.已知平行于x轴的直线分别交曲线y=e2x+1与y=$\sqrt{2x-1}$于A,B两点,则|AB|的最小值为( )
| A. | $\frac{5+ln2}{4}$ | B. | $\frac{5-ln2}{4}$ | C. | $\frac{3+ln2}{4}$ | D. | $\frac{3-ln2}{4}$ |
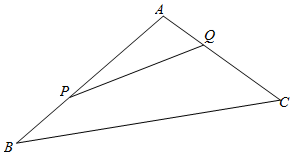 如图,上海迪士尼乐园将一三角形地块ABC的一角APQ开辟为游客体验活动区.已知∠A=120°,AB、AC的长度均大于200米.设AP=x,AQ=y,且AP,AQ总长度为200米.
如图,上海迪士尼乐园将一三角形地块ABC的一角APQ开辟为游客体验活动区.已知∠A=120°,AB、AC的长度均大于200米.设AP=x,AQ=y,且AP,AQ总长度为200米.