题目内容
设椭圆C: 过点(0,4),离心率为
过点(0,4),离心率为
(Ⅰ)求C的方程;
(Ⅱ)求过点(3,0)且斜率为
 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标.
【答案】分析:(Ⅰ)根据题意,将(0,4)代入C的方程得b的值,进而由椭圆的离心率为 ,结合椭圆的性质,可得
,结合椭圆的性质,可得 =
=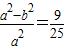 ;解可得a的值,将a、b的值代入方程,可得椭圆的方程.
;解可得a的值,将a、b的值代入方程,可得椭圆的方程.
(Ⅱ)根据题意,可得直线的方程,设直线与C的交点为A(x1,y1),B(x2,y2),联立直线与椭圆的方程,化简可得方程x2-3x-8=0,解可得x1与x2的值,由中点坐标公式可得中点的横坐标,将其代入直线方程,可得中点的纵坐标,即可得答案.
解答:解:(Ⅰ)根据题意,椭圆过点(0,4),
将(0,4)代入C的方程得 ,即b=4
,即b=4
又 得
得 =
= ;
;
即 ,∴a=5
,∴a=5
∴C的方程为
(Ⅱ)过点(3,0)且斜率为 的直线方程为
的直线方程为 ,
,
设直线与C的交点为A(x1,y1),B(x2,y2),
将直线方程 代入C的方程,得
代入C的方程,得 ,
,
即x2-3x-8=0,解得 ,
, ,
,
∴AB的中点坐标 ,
,
 ,
,
即中点为 .
.
点评:本题考查椭圆的性质以及椭圆与直线相交的有关性质,涉及直线与椭圆问题,一般要联立两者的方程,转化为一元二次方程,由韦达定理分析解决.
 ,结合椭圆的性质,可得
,结合椭圆的性质,可得 =
=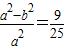 ;解可得a的值,将a、b的值代入方程,可得椭圆的方程.
;解可得a的值,将a、b的值代入方程,可得椭圆的方程.(Ⅱ)根据题意,可得直线的方程,设直线与C的交点为A(x1,y1),B(x2,y2),联立直线与椭圆的方程,化简可得方程x2-3x-8=0,解可得x1与x2的值,由中点坐标公式可得中点的横坐标,将其代入直线方程,可得中点的纵坐标,即可得答案.
解答:解:(Ⅰ)根据题意,椭圆过点(0,4),
将(0,4)代入C的方程得
 ,即b=4
,即b=4又
 得
得 =
= ;
;即
 ,∴a=5
,∴a=5∴C的方程为

(Ⅱ)过点(3,0)且斜率为
 的直线方程为
的直线方程为 ,
,设直线与C的交点为A(x1,y1),B(x2,y2),
将直线方程
 代入C的方程,得
代入C的方程,得 ,
,即x2-3x-8=0,解得
 ,
, ,
,∴AB的中点坐标
 ,
, ,
,即中点为
 .
.点评:本题考查椭圆的性质以及椭圆与直线相交的有关性质,涉及直线与椭圆问题,一般要联立两者的方程,转化为一元二次方程,由韦达定理分析解决.

练习册系列答案
相关题目
 过点(0,4),离心率为
过点(0,4),离心率为 .
. 的直线被C所截得线段的中点坐标.
的直线被C所截得线段的中点坐标.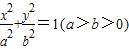 过点(0,4),离心率为
过点(0,4),离心率为
 过点(0,4),离心率为
过点(0,4),离心率为
 过点(0,4),离心率为
过点(0,4),离心率为
 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标.