题目内容
设椭圆C: 过点(0,4),离心率为
过点(0,4),离心率为
(Ⅰ)求C的方程;
(Ⅱ)求过点(3,0)的动直线被C所截线段的中点轨迹方程.
【答案】分析:(Ⅰ)由椭圆C: 过点(0,4),离心率为
过点(0,4),离心率为 ,知
,知 ,由此能求出椭圆C的方程.
,由此能求出椭圆C的方程.
(Ⅱ)设过点(3,0)的直线交椭圆 于A(x1,y1),B(x2,y2),设AB的中点为M(x,y),利用点差法能够求出过点(3,0)的动直线被C所截线段的中点轨迹方程.
于A(x1,y1),B(x2,y2),设AB的中点为M(x,y),利用点差法能够求出过点(3,0)的动直线被C所截线段的中点轨迹方程.
解答:解:(Ⅰ)∵椭圆C: 过点(0,4),离心率为
过点(0,4),离心率为 ,
,
∴ ,解得a=5,b=4,c=3,
,解得a=5,b=4,c=3,
∴椭圆C的方程是 .
.
(Ⅱ)设过点(3,0)的直线交椭圆 于A(x1,y1),B(x2,y2),
于A(x1,y1),B(x2,y2),
设AB的中点为M(x,y),则x1+x2=2x,y1+y2=2y,
把A(x1,y1),B(x2,y2)代入椭圆16x2+25y2=400,
得
①-②,得16(x1+x2)(x1-x2)+25(y1+y2)(y1-y2)=0,
∴32x(x1-x2)+50y(y1-y2)=0,
∴直线AB的斜率k= =-
=- ,
,
∵直线AB过点(3,0),M(x,y),
∴直线AB的斜率k= ,
,
∴- =
= ,整理,得16x2+25y2-48x=0.
,整理,得16x2+25y2-48x=0.
当k不存在时,16x2+25y2-48x=0也成立.
故过点(3,0)的动直线被C所截线段的中点轨迹方程是16x2+25y2-48x=0.
点评:本题考查椭圆方程的求法,考查点的轨迹方程的求法,解题时要认真审题,仔细解答,注意点差法的合理运用.
 过点(0,4),离心率为
过点(0,4),离心率为 ,知
,知 ,由此能求出椭圆C的方程.
,由此能求出椭圆C的方程.(Ⅱ)设过点(3,0)的直线交椭圆
 于A(x1,y1),B(x2,y2),设AB的中点为M(x,y),利用点差法能够求出过点(3,0)的动直线被C所截线段的中点轨迹方程.
于A(x1,y1),B(x2,y2),设AB的中点为M(x,y),利用点差法能够求出过点(3,0)的动直线被C所截线段的中点轨迹方程.解答:解:(Ⅰ)∵椭圆C:
 过点(0,4),离心率为
过点(0,4),离心率为 ,
,∴
 ,解得a=5,b=4,c=3,
,解得a=5,b=4,c=3,∴椭圆C的方程是
 .
.(Ⅱ)设过点(3,0)的直线交椭圆
 于A(x1,y1),B(x2,y2),
于A(x1,y1),B(x2,y2),设AB的中点为M(x,y),则x1+x2=2x,y1+y2=2y,
把A(x1,y1),B(x2,y2)代入椭圆16x2+25y2=400,
得

①-②,得16(x1+x2)(x1-x2)+25(y1+y2)(y1-y2)=0,
∴32x(x1-x2)+50y(y1-y2)=0,
∴直线AB的斜率k=
 =-
=- ,
,∵直线AB过点(3,0),M(x,y),
∴直线AB的斜率k=
 ,
,∴-
 =
= ,整理,得16x2+25y2-48x=0.
,整理,得16x2+25y2-48x=0.当k不存在时,16x2+25y2-48x=0也成立.
故过点(3,0)的动直线被C所截线段的中点轨迹方程是16x2+25y2-48x=0.
点评:本题考查椭圆方程的求法,考查点的轨迹方程的求法,解题时要认真审题,仔细解答,注意点差法的合理运用.

练习册系列答案
相关题目
 过点(0,4),离心率为
过点(0,4),离心率为 .
. 的直线被C所截得线段的中点坐标.
的直线被C所截得线段的中点坐标.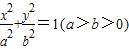 过点(0,4),离心率为
过点(0,4),离心率为
 过点(0,4),离心率为
过点(0,4),离心率为
 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标. 过点(0,4),离心率为
过点(0,4),离心率为
 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标.