题目内容

函数f(x)=Asin(ωx+
π
6
)(ω＞0)的图象与x轴的交点的横坐标构成一个公差为
π
2
的等差数列，要得到函数g（x）=Acosωx的图象只需将f（x）的图象向左左平移
π
6
π
6
一个单位长度．
根据函数f(x)=Asin(ωx+
π
6
)(ω＞0)的图象与x轴的交点的横坐标构成一个公差为
π
2
的等差数列，可得函数的周期为π，
即
2π
ω
=π，∴ω=2，∴f（x）=Asin（2x+
π
6
 ）．
再由函数g（x）=Acos2x=Asin（2x+
π
2
）=Asin[2（x+
π
6
）+
π
6
]，
故把f（x）=Asin（2x+
π
6
 ） 的图象向左平移
π
6
个单位，可得函数g（x）=Acos2x=Asin[2（x+
π
6
）+
π
6
]的图象，
故答案为 左；
π
6
．
练习册系列答案
相关题目
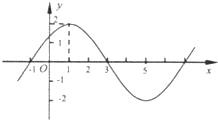精英家教网已知函数f(x)=Asin(ωx+φ)，(A＞0，ω＞0，|φ|＜
π2
，x∈R)的图象的一部分如图所示，则函数f（x）的解析式为
 
．
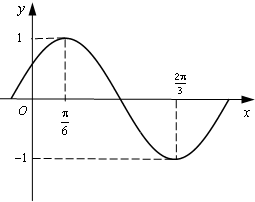精英家教网函数f(x)=Asin(ωx+?) (A＞0，ω＞0，|?|＜
π
2
)部分图象如图所示．
（Ⅰ）求f（x）的最小正周期及解析式；
（Ⅱ）设g（x）=f（x）-cos2x，求函数g（x）在区间x∈[0，
π
2
]上的最大值和最小值．
已知函数f(x)=Asin(ωx+?)，x∈R，(A＞0．ω＞0，0＜?＜
π
2
)的图象与x轴的交点中，相邻两个交点之间的距离为
π
2
，且图象上一个最低点为M(
2π
3
，-2)．
（1）求f（x）的解析式；
（2）设A，B，C是△ABC的三个内角，若cosB=
1
3
，f(
C
2
)=
3
，求sinA．
函数f(x)=Asin(ωx-
π
6
)（A＞0，ω＞0）的最大值为2，其最小正周期为π．
（1）求函数f（x）的解析式；
（2）设α∈(0，
π
2
)，则f(
α
2
)=
2
，求cosα的值．
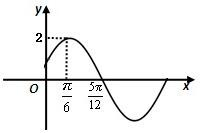（2010•广东模拟）已知函数f(x)=Asin(ωx+φ)(A＞0，ω＞0，|φ|＜
π
2
)的部分图象如图所示．
（1）求函数f（x）的解析式；
（2）令g(x)=f(x+
π
12
)，判断函数g（x）的奇偶性，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网