题目内容
已知向量 =(sinθ,1),
=(sinθ,1), =(1,-cosθ),θ∈(0,π)
=(1,-cosθ),θ∈(0,π)
(Ⅰ)若 ,求θ;
,求θ;
(Ⅱ)若 ,求
,求 的值.
的值.
解:(I)∵
∴sinθ-cosθ=0即tanθ=1
∵θ∈(0,π)
∴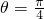
(II)由 平方得2
平方得2
∴
∴sinθ+cosθ=
得
得 .
.
分析:(I)利用向量垂直的充要条件:数量积等于0,列出方程,解三角方程求出角.
(II)利用向量的数量积公式得到三角方程 ,利用三角函数的平方关系求出sinθ+cosθ;解方程组求出正弦、余弦,进而得到正切;利用二倍角公式及和角公式求出值.
,利用三角函数的平方关系求出sinθ+cosθ;解方程组求出正弦、余弦,进而得到正切;利用二倍角公式及和角公式求出值.
点评:本题考查向量垂直的充要条件、三角函数的平方关系、二倍角的正切公式及和角的正切公式.

∴sinθ-cosθ=0即tanθ=1
∵θ∈(0,π)
∴
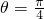
(II)由
 平方得2
平方得2
∴

∴sinθ+cosθ=

得

得
 .
.分析:(I)利用向量垂直的充要条件:数量积等于0,列出方程,解三角方程求出角.
(II)利用向量的数量积公式得到三角方程
 ,利用三角函数的平方关系求出sinθ+cosθ;解方程组求出正弦、余弦,进而得到正切;利用二倍角公式及和角公式求出值.
,利用三角函数的平方关系求出sinθ+cosθ;解方程组求出正弦、余弦,进而得到正切;利用二倍角公式及和角公式求出值.点评:本题考查向量垂直的充要条件、三角函数的平方关系、二倍角的正切公式及和角的正切公式.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目