题目内容
已知A(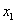 ,
,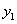 ),B(
),B(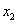 ,
,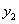 )是函数
)是函数 的图象上的任意两点(可以重合),点M在直线
的图象上的任意两点(可以重合),点M在直线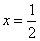 上,且
上,且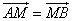 .
.
(1)求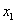 +
+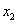 的值及
的值及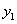 +
+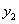 的值
的值
(2)已知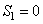 ,当
,当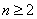 时,
时,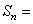
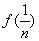 +
+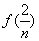 +
+ +
+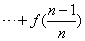 ,求
,求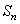 ;
;
(3)在(2)的条件下,设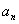 =
=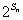 ,
,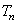 为数列{
为数列{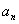 }的前
}的前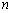 项和,若存在正整数
项和,若存在正整数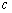 、
、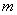 ,
,
使得不等式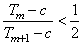 成立,求
成立,求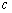 和
和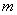 的值.
的值.
【答案】
(1) +
+ . (2)
. (2) ="1-n."
(3)c="1,"
m=1.
="1-n."
(3)c="1,"
m=1.
【解析】
试题分析:(Ⅰ)∵点M在直线x= 上,设M
上,设M .
.
又 =
= ,即
,即 ,
, ,
,
∴ +
+ ="1."
="1."
① 当 =
= 时,
时, =
= ,
, +
+ =
= ;
;
② 当

 时,
时,

 ,
,
 +
+ =
= +
+ =
= =
= =
=
综合①②得, +
+ .
.
(Ⅱ)由(Ⅰ)知,当 +
+ =1时,
=1时,  +
+
∴ ,k=
,k= .
.
n≥2时,
 +
+ +
+ +
+ , ①
, ①

 , ②
, ②
②得,2 =-2(n-1),则
=-2(n-1),则 =1-n.
=1-n.
当n=1时, =0满足
=0满足 ="1-n."
∴
="1-n."
∴ ="1-n."
="1-n."
(Ⅲ) =
= =
= ,
, =1+
=1+ +
+ =
= .
.




 .
.
 =2-
=2- ,
, =
= -2+
-2+ =2-
=2- ,∴
,∴
 ,
, 、m为正整
、m为正整
数,∴c=1,当c=1时, ,
,
∴1< <3,
<3,
∴m=1.
考点:分段函数的解析式求法及其图象的作法;数列的求和;数列递推式;相等向量与相反
向量.
点评:本题考查分段函数,数列的求和,数列递推式,相等向量与相反向量,考查学生分析
问题解决问题的能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,已知a=8,B=60°,A=45°,则b等于( )
A、4
| ||
B、4
| ||
C、4
| ||
D、
|