题目内容
如图所示,中心在原点,顶点A1、A2在x轴上,离心率为的双曲线C经过点P (6 , 6),
动直线l经过点(0 , 1)与双曲线C交于M、N两点,Q为线段MN的中点.
 (1) 求双曲线C的标准方程;
(1) 求双曲线C的标准方程;
(2) 若E点为(1 , 0),是否存在实数λ使 =λ,若存在,
求λ值;若不存在,说明理由.
【答案】
解:(1)
设双曲线为: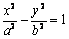 (a
>0,b >0),
(a
>0,b >0),
由 = 得:b2
= a2,∵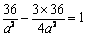 .∴a2 = 9,b2 = 12.
.∴a2 = 9,b2 = 12.
∴所求方程为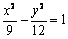 .
(4分)
.
(4分)
(2) 设M(x1 , y1 ),N(x2 , y2 ),Q(x0 , y0 ),l:y = kx + 1.
由得:(k2)xkx - 39 = 0. ∴得:
- < k <
,且k≠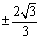 .
(6分)
.
(6分)
又x1 + x2
=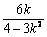 ,x0 = =
,x0 = =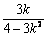 ,y0= kx0+1=
,y0= kx0+1=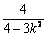
∴Q(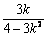 ,
,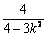 ).∴ = (
).∴ = (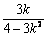 -1,
-1,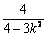 ), = (3 , 6). (8分)
), = (3 , 6). (8分)
而 =λ,∴6(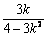 -1)- 3×
-1)- 3×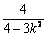 =0.
∴k2+k - 2 = 0,
=0.
∴k2+k - 2 = 0,
∴k = 1或-2. (10分)
而-2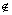 (- , ),∴k =1, =(2 , 4),∴3λ=
2,λ= ,
(- , ),∴k =1, =(2 , 4),∴3λ=
2,λ= ,
∴λ存在,值为,使 =λ. (12分)

练习册系列答案
相关题目
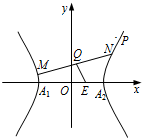 如图所示,中心在原点,顶点A1、A2在x轴上,离心率为
如图所示,中心在原点,顶点A1、A2在x轴上,离心率为

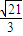 的双曲线C经过点P (6,6),动直线l经过点(0,1)与双曲线C交于M、N两点,Q为线段MN的中点.
的双曲线C经过点P (6,6),动直线l经过点(0,1)与双曲线C交于M、N两点,Q为线段MN的中点. =λ
=λ ,若存在,求λ值;若不存在,说明理由.
,若存在,求λ值;若不存在,说明理由.