题目内容
如图所示,中心在原点,顶点A1、A2在x轴上,离心率为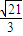 的双曲线C经过点P (6,6),动直线l经过点(0,1)与双曲线C交于M、N两点,Q为线段MN的中点.
的双曲线C经过点P (6,6),动直线l经过点(0,1)与双曲线C交于M、N两点,Q为线段MN的中点.(1)求双曲线C的标准方程;
(2)若E点为(1,0),是否存在实数λ使
 =λ
=λ ,若存在,求λ值;若不存在,说明理由.
,若存在,求λ值;若不存在,说明理由.
【答案】分析:(1)由双曲线的离心率为 知,
知, ,根据双曲线C经过点P (6,6),知P点坐标满足双曲线方程,代入,又得到一个含a,b的等式,再根据a,b,c的关系式,可解出a,b,求出双曲线C的标准方程.
,根据双曲线C经过点P (6,6),知P点坐标满足双曲线方程,代入,又得到一个含a,b的等式,再根据a,b,c的关系式,可解出a,b,求出双曲线C的标准方程.
(2)先假设存在实数λ使 =λ
=λ ,设出M,N,点的坐标,再用M,N点坐标表示Q点坐标,设直线l的方程,把直线l的方程代入(1)中所求双曲线方程,求x1+x2,x1x2,根据
,设出M,N,点的坐标,再用M,N点坐标表示Q点坐标,设直线l的方程,把直线l的方程代入(1)中所求双曲线方程,求x1+x2,x1x2,根据 =λ
=λ ,可得关于k的方程,解方程,若能求出k值,则存在,若不能求出,则不存在.
,可得关于k的方程,解方程,若能求出k值,则存在,若不能求出,则不存在.
解答:解:(1)设双曲线为: (a>0,b>0),
(a>0,b>0),
由 =
= 得:b2=
得:b2= a2,∵
a2,∵ .∴a2=9,b2=12.
.∴a2=9,b2=12.
∴所求方程为 .
.
(2)设M(x1,y1 ),N(x2,y2 ),Q(x,y ),l:y=kx+1.
由 得:(4-3k2)x2-6kx-39=0.∴
得:(4-3k2)x2-6kx-39=0.∴ 得:
得:
- <k<
<k< ,且k≠
,且k≠ .
.
又x1+x2= ,x=
,x= =
= ,y=kx+1=
,y=kx+1=
∴Q( ,
, ).∴
).∴ =(
=( -1,
-1, ),
), =(3,6).
=(3,6).
而 ,∴6(
,∴6( -1)-3×
-1)-3× =0.∴k2+k-2=0,
=0.∴k2+k-2=0,
∴k=1或-2.
而-2∉(- ,
, ),∴k=1,
),∴k=1, =(2,4),∴3λ=2,λ=
=(2,4),∴3λ=2,λ= ,
,
∴λ存在,值为 ,使
,使 .
.
点评:本题主要考查了双曲线方程的求法,以及向量与圆锥曲线的综合来解存在性问题.
 知,
知, ,根据双曲线C经过点P (6,6),知P点坐标满足双曲线方程,代入,又得到一个含a,b的等式,再根据a,b,c的关系式,可解出a,b,求出双曲线C的标准方程.
,根据双曲线C经过点P (6,6),知P点坐标满足双曲线方程,代入,又得到一个含a,b的等式,再根据a,b,c的关系式,可解出a,b,求出双曲线C的标准方程.(2)先假设存在实数λ使
 =λ
=λ ,设出M,N,点的坐标,再用M,N点坐标表示Q点坐标,设直线l的方程,把直线l的方程代入(1)中所求双曲线方程,求x1+x2,x1x2,根据
,设出M,N,点的坐标,再用M,N点坐标表示Q点坐标,设直线l的方程,把直线l的方程代入(1)中所求双曲线方程,求x1+x2,x1x2,根据 =λ
=λ ,可得关于k的方程,解方程,若能求出k值,则存在,若不能求出,则不存在.
,可得关于k的方程,解方程,若能求出k值,则存在,若不能求出,则不存在.解答:解:(1)设双曲线为:
 (a>0,b>0),
(a>0,b>0),由
 =
= 得:b2=
得:b2= a2,∵
a2,∵ .∴a2=9,b2=12.
.∴a2=9,b2=12.∴所求方程为
 .
.(2)设M(x1,y1 ),N(x2,y2 ),Q(x,y ),l:y=kx+1.
由
 得:(4-3k2)x2-6kx-39=0.∴
得:(4-3k2)x2-6kx-39=0.∴ 得:
得:-
 <k<
<k< ,且k≠
,且k≠ .
.又x1+x2=
 ,x=
,x= =
= ,y=kx+1=
,y=kx+1=
∴Q(
 ,
, ).∴
).∴ =(
=( -1,
-1, ),
), =(3,6).
=(3,6).而
 ,∴6(
,∴6( -1)-3×
-1)-3× =0.∴k2+k-2=0,
=0.∴k2+k-2=0,∴k=1或-2.
而-2∉(-
 ,
, ),∴k=1,
),∴k=1, =(2,4),∴3λ=2,λ=
=(2,4),∴3λ=2,λ= ,
,∴λ存在,值为
 ,使
,使 .
.点评:本题主要考查了双曲线方程的求法,以及向量与圆锥曲线的综合来解存在性问题.

练习册系列答案
相关题目
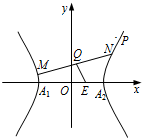 如图所示,中心在原点,顶点A1、A2在x轴上,离心率为
如图所示,中心在原点,顶点A1、A2在x轴上,离心率为

 (1) 求双曲线C的标准方程;
(1) 求双曲线C的标准方程;