题目内容
关于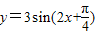 有如下说法:
有如下说法:①若f(x1)=f(x2)=0,则x1-x2是π的整数倍,
②函数解析式可改为
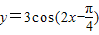 ,
,③函数图象关于
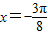 对称,
对称,④函数图象关于点
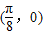 对称.
对称.其中正确的是 (填正确的序号)
【答案】分析:①若f(x1)=f(x2)=0,则x1-x2是半个周期的整数倍,故不正确.
②利用诱导公式可得,函数解析式可化为 ,故正确.
,故正确.
③当 时,y=-3,是函数的最小值,故正确.④当 x=
时,y=-3,是函数的最小值,故正确.④当 x=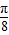 时,y=3,是函数的最大值,故不正确.
时,y=3,是函数的最大值,故不正确.
解答:解:①若f(x1)=f(x2)=0,则x1-x2是半个周期的整数倍,函数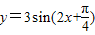 的周期为π,故x1-x2是
的周期为π,故x1-x2是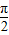 的整数倍,故①不正确.
的整数倍,故①不正确.
②函数解析式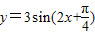 =3cos[
=3cos[ -(2x+
-(2x+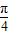 )]=
)]= =
=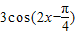 ,故②正确.
,故②正确.
③当 时,y=-3,是函数的最小值,故函数图象关于
时,y=-3,是函数的最小值,故函数图象关于 对称,故③正确.
对称,故③正确.
④当 x= 时,y=3,是函数的最大值,故函数图象关于x=
时,y=3,是函数的最大值,故函数图象关于x= 对称,故④不正确.
对称,故④不正确.
故答案为:②③.
点评:本题考查正弦函数的对称性、周期性,诱导公式的应用,掌握函数 的图象性质,是解题的关键.
的图象性质,是解题的关键.
②利用诱导公式可得,函数解析式可化为
 ,故正确.
,故正确.③当
 时,y=-3,是函数的最小值,故正确.④当 x=
时,y=-3,是函数的最小值,故正确.④当 x=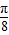 时,y=3,是函数的最大值,故不正确.
时,y=3,是函数的最大值,故不正确.解答:解:①若f(x1)=f(x2)=0,则x1-x2是半个周期的整数倍,函数
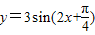 的周期为π,故x1-x2是
的周期为π,故x1-x2是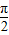 的整数倍,故①不正确.
的整数倍,故①不正确.②函数解析式
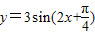 =3cos[
=3cos[ -(2x+
-(2x+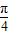 )]=
)]= =
=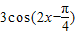 ,故②正确.
,故②正确.③当
 时,y=-3,是函数的最小值,故函数图象关于
时,y=-3,是函数的最小值,故函数图象关于 对称,故③正确.
对称,故③正确.④当 x=
 时,y=3,是函数的最大值,故函数图象关于x=
时,y=3,是函数的最大值,故函数图象关于x= 对称,故④不正确.
对称,故④不正确.故答案为:②③.
点评:本题考查正弦函数的对称性、周期性,诱导公式的应用,掌握函数
 的图象性质,是解题的关键.
的图象性质,是解题的关键. 
练习册系列答案
相关题目
 有如下说法:
有如下说法: ,
, 对称,
对称, 对称.
对称.