题目内容
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,且椭圆
,且椭圆![]() 过点
过点 .过点
.过点![]() 做两条相互垂直的直线
做两条相互垂直的直线![]() 、
、![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() 、
、![]() 、
、![]() 、
、![]() 四点.
四点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若![]() ,
, ![]() ,探究:直线
,探究:直线![]() 是否过定点?若是,请求出定点坐标;若不是,请说明理由.
是否过定点?若是,请求出定点坐标;若不是,请说明理由.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(Ⅰ)由已知,可建立关于椭圆三个参数![]() 的方程组进行求解,由离心率可得
的方程组进行求解,由离心率可得![]() ,又点
,又点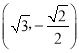 在椭圆上,可得
在椭圆上,可得![]() ,结合
,结合![]() ,从而问题可得解.
,从而问题可得解.
(Ⅱ)由题意,可对直线![]() 的斜率分“不存在与0”和“都存在且
的斜率分“不存在与0”和“都存在且![]() ”两种情况进行分类讨论,先对后一种情况探究,则可设两直线的方程分别为
”两种情况进行分类讨论,先对后一种情况探究,则可设两直线的方程分别为![]() ,
, ![]() ,逐个联立椭圆方程,分别计算
,逐个联立椭圆方程,分别计算![]() 的中点
的中点![]() 的坐标,从而求出直线
的坐标,从而求出直线![]() 的方程,并求得其定点为
的方程,并求得其定点为![]() ,再对前一种情况进行验证即可.
,再对前一种情况进行验证即可.
试题解析:(Ⅰ)由题意知, 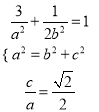 ,解得
,解得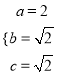 ,
,
故椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)∵![]() ,
, ![]() ,∴
,∴![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
当两直线的斜率都存在且不为0时,设直线![]() 的方程为
的方程为![]() ,
,
则直线![]() 的方程为
的方程为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
联立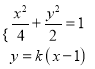 ,得
,得![]() ,∴
,∴![]() ,
,
∴![]() ,
, ![]() ,∴
,∴![]() 中点
中点![]() 的坐标为
的坐标为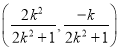 ;
;
同理, ![]() 中点
中点![]() 的坐标为
的坐标为![]() ,∴
,∴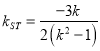 ,
,
∴直线![]() 的方程为
的方程为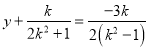
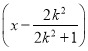 ,
,
即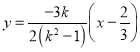 ,∴直线
,∴直线![]() 过定点
过定点![]() ;
;
当两直线的斜率分别为0和不存在时,则直线![]() 的方程为
的方程为![]() ,也过点
,也过点![]() ;
;
综上所述,直线![]() 过定点
过定点![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



