题目内容
如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB//CD,AB=AD= ,点M在线段EC上且不与E、C垂合.
,点M在线段EC上且不与E、C垂合.
(1)当点M是EC中点时,求证:BM//平面ADEF;
(2)当平面BDM与平面ABF所成锐二面角的余弦值为 时,求三棱锥M—BDE的体积
时,求三棱锥M—BDE的体积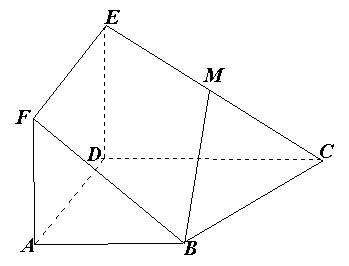
(1)详见解析;(2)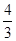
解析试题分析:以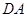 、
、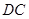 、
、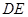 分别为
分别为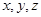 轴建立空间直角坐如图,
轴建立空间直角坐如图,
(1)要证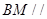 面
面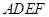 ,只要证明向量
,只要证明向量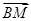 与平面
与平面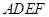 的法向量
的法向量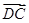 垂直即可;
垂直即可;
(2)设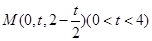 ,设面
,设面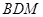 的法向量
的法向量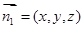 ,
,
利用向量的数量积求得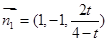 ,而平面
,而平面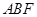 的法向量
的法向量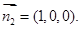
由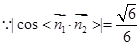 ,解出
,解出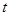 的值,从而确定点
的值,从而确定点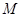 位置,进而求出
位置,进而求出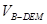 也即三棱锥M—BDE的体积.
也即三棱锥M—BDE的体积.
试题解析: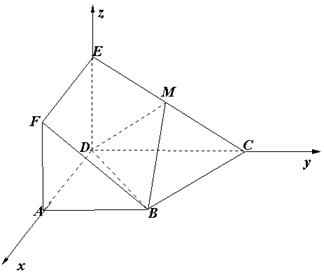
(1)以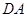 、
、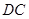 、
、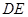 分别为
分别为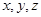 轴建立空间直角坐标系
轴建立空间直角坐标系
则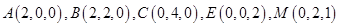
所以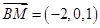 ,面
,面 的一个法向量
的一个法向量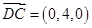
所以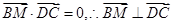 ,即
,即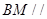 面
面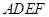 4分
4分
(2)依题意设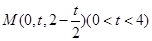 ,设面
,设面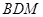 的法向量
的法向量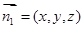
则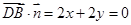 ,
,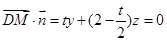
令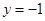 ,则
,则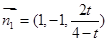 ,面
,面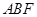 的法向量
的法向量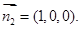
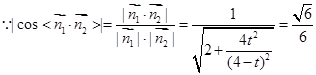 ,解得
,解得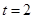
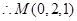 为EC的中点,
为EC的中点,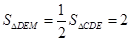 ,
,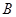 到面
到面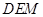 的距离
的距离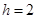
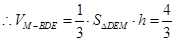 12分
12分
考点:1、空间直角坐标系;2、向量法解决空间的平行、垂直与夹角问题;3、空间几何体的体积.

练习册系列答案
相关题目
 为圆
为圆 的直径,
的直径, 为圆周上异于
为圆周上异于 、
、 的一点,
的一点, 垂直于圆
垂直于圆 于
于 ,
, 于点
于点 .
. 平面
平面 ;
; ,
, ,求四面体
,求四面体 的体积.
的体积.
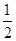 PD.
PD.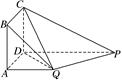
 为矩形,
为矩形,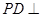 平面
平面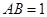 ,
,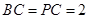 ,作如图3折叠,折痕
,作如图3折叠,折痕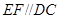 .其中点
.其中点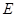 、
、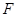 分别在线段
分别在线段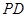 、
、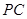 上,沿
上,沿 折叠后点
折叠后点 在线段
在线段 上的点记为
上的点记为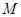 ,并且
,并且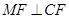 .
.
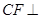 平面
平面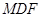 ;
;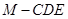 的体积.
的体积.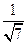 ,求三棱锥E-PAB的体积.
,求三棱锥E-PAB的体积.
 中,
中, ,
, ,
, ,在三角形内挖去一个半圆(圆心
,在三角形内挖去一个半圆(圆心 在边
在边 上,半圆与
上,半圆与 、
、 分别相切于点
分别相切于点 、
、 ,与
,与 ),将△
),将△
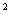 ,则此球的体积为____
,则此球的体积为____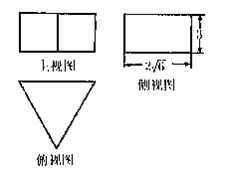
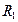 ,
,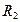 ,
,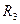 满足
满足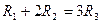 ,则它们的表面积
,则它们的表面积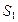 ,
,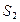 ,
,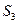 ,满足的等量关系是___________.
,满足的等量关系是___________.