题目内容
5.集合M是具有以下性质的函数f(x)的全体:对于任意a,b>0,都有f(a)>0,f(b)>0,且f(a)+f(b)<f(a+b).(1)试判断函数f(x)=2x-1是否属于集合M?
(2)证明:集合M中的函数f(x)在区间(0,+∞)上是增函数.
分析 (1)a>0,b>0时,容易得出f(a)>0,f(b)>0,然后判断f(a)+f(b)<f(a+b)是否成立,可作差,提取公因式,便可得出f(a)+f(b)-f(a+b)=(2a-1)(1-2b)<0,这样便可得出f(a)+f(b)<f(a+b),从而得出该函数属于集合M;
(2)已知f(x)∈M,可根据增函数的定义来证明f(x)在(0,+∞)上是增函数:设任意的x1>x2>0,这样便可设x1=x2+x0,x0>0,然后作差,根据集合M中的函数所满足的条件即可证明f(x1)>f(x2),从而得出f(x)在(0,+∞)上是增函数.
解答 解:(1)任意的a,b>0,都有f(a)=2a-1>0,f(b)=2b-1>0;
f(a)+f(b)-f(a+b)=2a-1+2b-1-2a+b+1=2a-1+2b-2a+b=(2a-1)(1-2b);
∵a>0,b>0;
∴2a-1>0,1-2b<0;
∴f(a)+f(b)<f(a+b);
∴f(x)=2x-1属于集合M;
(2)证明:设f(x)∈M,设x1>x2>0,则存在x0使x1=x2+x0;
∴f(x1)-f(x2)=f(x2+x0)-f(x2)>f(x2)+f(x0)-f(x2)=f(x0)>0;
∴f(x1)>f(x2);
∴f(x)在(0,+∞)上是增函数.
点评 考查指数函数的单调性,作差法比较两个数的大小,增函数的定义,以及根据增函数的定义证明函数单调性的方法,作差法比较f(x1)与f(x2),作差之后一般要提取公因式,从而判断差的符号,以及对于集合M中函数所满足条件的运用.

练习册系列答案
相关题目
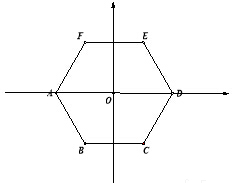 已知正六边形ABCDEF的边长是2,以正六边形中心为原点,以对角线AD所在的直线为x轴,如图建立平面直角坐标系.
已知正六边形ABCDEF的边长是2,以正六边形中心为原点,以对角线AD所在的直线为x轴,如图建立平面直角坐标系.