题目内容

19．已知f（x）=$\left\{\begin{array}{l}{x-6，（x≥6）}\\{f（x+2），（x＜6）}\end{array}\right.$，则f（3）为（　　）
A．1B．2C．4D．5

分析 直接利用分段函数的解析式求解函数值即可．

解答 解：f（x）=$\left\{\begin{array}{l}{x-6，（x≥6）}\\{f（x+2），（x＜6）}\end{array}\right.$，
则f（3）=f（5）=f（7）=7-6=1．
故选：A．

点评 本题考查函数的解析式的应用，函数值的求法，是基础题．

练习册系列答案
相关题目
9．数列{an}的通项公式an=ncos$\frac{nπ}{2}$+1，前n项和为Sn，则S1=1，S2015=1007．
10．设函数f（x）=ex（2x-1）+ax-a，其中a＞-1，若关于x不等式f（x）＜0的整数解有且只有一个，则实数a的取值范围为（　　）
A．（-1，$\frac{3}{2e}$]B．（-$\frac{3}{4}$，$\frac{3}{2e}$]C．（-$\frac{3}{4}$，-$\frac{3}{2e}$]D．（-1，-$\frac{3}{2e}$]
7．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-3tx+18，x≤3}\\{（t-13）\sqrt{x-3}，x＞3}\end{array}\right.$，记an=f（n）（n∈N*），若数列{an}满足an＞an+1，则实数t的取值范围是（$\frac{5}{3}$，4）．
14．已知i是虚数单位，若$z=\frac{a+i}{{a+{i^{2015}}}}$是纯虚数，则实数a的值为（　　）
A．1B．±1C．2D．±2
4．（1）已知tan（3π+α）=3，试求$\frac{sin（α-3π）+cos（π-α）+sin（\frac{π}{2}-α）-2cos（\frac{π}{2}+α）}{-sin（-α）+cos（π+α）}$的值．
（2）已知角α的终边经过点P（-4，3），求sinαcosα+cos2α-sin2α+1的值．
11．已知定义在R上的函数f（x）的图象关于点（-$\frac{3}{4}$，0）成中心对称图形，且满足$f（x）=-f（x+\frac{3}{2}）$，f（-1）=1，f（0）=-2，则f（1）+f（2）+…+f（2015）的值为（　　）
A．1B．2C．-1D．-2
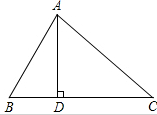8．如图，在△ABC中，AD⊥BC，$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$•$\frac{\overrightarrow{AC}}{|\overrightarrow{AC|}}$=$\frac{\sqrt{2}}{2}$，BD=4，CD=6．
（1）求∠BAC的大小；
（2）求边AC、AB的长．
9．已知幂函数f（x）=x${\;}^{{m}^{2}-2m-3}$，m∈{m|-1＜m＜3，m∈Z}，在区间（0，+∞）上是减函数，求f（x）的解析式并求其定义域、值域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网