题目内容
【题目】在平面直角坐标系xOy中，已知点A（﹣1，0），B（1，1），C（2，0），点P是平面直角坐标系xOy上一点，且 
=m 
（m，n∈R），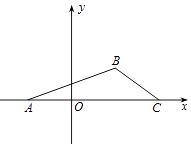
（1）若m=1，且 ∥ 
，试求实数n的值；
（2）若点P在△ABC三边围成的区域（含边界）上，求m+3n的最大值．
【答案】
（1）解：由题设知： 
， 
，
∵m=1，
所以： 
，
又∵ 
， 
，
∴2+3n=﹣1，得n=﹣1，
所以，满足题意的实数n=﹣1
（2）解：设P（x，y），
…
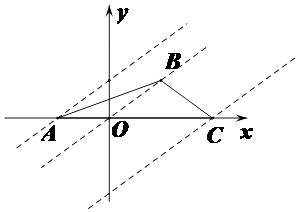
∴令： 
，
∴ 
，
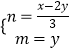∴m+3n=x﹣y，
令z=x﹣y，由图知，
当直线y=x﹣z过点C（2，0）时，
z取得最大值2，
故m+3n的最大值为2
【解析】（1）直接利用向量的线性运算求出对应的值，（2）利用线性规划问题求出对应的结果.
【考点精析】利用平面向量的基本定理及其意义对题目进行判断即可得到答案，需要熟知如果
、
是同一平面内的两个不共线向量，那么对于这一平面内的任意向量
，有且只有一对实数
、
，使
．
练习册系列答案
相关题目
