题目内容
函数y=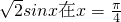
处的切线方程为________．
x-y+1-
=0
分析：先求导函数，利用导函数在x=
处可知切线的斜率，进而求出切点的坐标，即可求得切线方程．
解答：由题意，设f（x）=
sinx，∴f′（x）=cosx
当x=时，f′（）=×
=1，
∵x=时，y=sin=1
∴正弦函数y=sinx在x=处的切线方程为y-1=1×（x-）
即x-y+1-=0．
故答案为：x-y+1-=0．
点评：本题以正弦函数为载体，考查导数的几何意义，解题的关键是利用导数在切点的函数值为切线的斜率．
=0分析：先求导函数，利用导函数在x=
处可知切线的斜率，进而求出切点的坐标，即可求得切线方程．解答：由题意，设f（x）=
sinx，∴f′（x）=cosx当x=
时，f′（）=×=1，∵x=
时，y=sin=1∴正弦函数y=
sinx在x=处的切线方程为y-1=1×（x-）即x-y+1-
=0．故答案为：x-y+1-
=0．点评：本题以正弦函数为载体，考查导数的几何意义，解题的关键是利用导数在切点的函数值为切线的斜率．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
函数
在
处的切线方程是
[
]|
A ．y=4x |
B ．y=4x－4 |
|
C ．y=4x＋4 |
D ．y=2x－4 |
曲线
处的切线方程为y=1。