Question

【题目】已知矩形ABCD中，E、F分别是AB、CD上的点，BE=CF=1，BC=2，AB=CD=3，P、Q分别为DE、CF的中点，现沿着EF翻折，使得二面角A﹣EF﹣B大小为 ．
（Ⅰ）求证：PQ∥平面BCD；
（Ⅱ）求二面角A﹣DB﹣E的余弦值．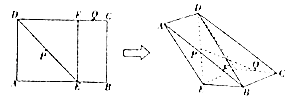

Answer 1

【答案】证明：（Ⅰ）取EB的中点M，连接PM，QM， ∵P为DE的中点，
∴PM∥BD，
∵PM平面BCD，BD平面BCD，
∴PM∥平面BCD，
同理MQ∥平面BCD，
∵PM∩MQ=M，
∴平面PMQ∥平面BCD，
∵PQ平面PQM，
∴PQ∥平面BCD；
（Ⅱ）解：在平面DFC内，过F作FC的垂线，则∠DFC= ，建立坐标系，则E（2，0，0），C（0，1，0），B（2，1，0），D（0，﹣1，﹣ ），A（2，﹣1， ），
∴ =（﹣2，﹣2， ）， =（0，2，﹣ ）， =（0，1，0），
设平面DAB的一个法向量为 =（x，y，z），则 ，取 =（0， ， ），
同理平面DBE的一个法向量为 =（ ，0， ），
∴cos＜ ， ＞= = ，
∴二面角A﹣DB﹣E的余弦值为 ．

【解析】（Ⅰ）取EB的中点M，连接PM，QM，证明：平面PMQ∥平面BCD，即可证明PQ∥平面BCD；（Ⅱ）建立坐标系，利用向量方法，即可求二面角A﹣DB﹣E的余弦值．
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．