题目内容
三棱柱OAB—O1A1B1中，平面OBB1O1⊥平面OAB，∠O1OB=60°，∠AOB=90°且OB=OO1=2，OA=
.求异面直线A1B与AO1所成角的大小.
解析：以O为原点，分别以直线OA、OB为x轴、y轴，过O点且与平面AOB垂直的直线为z轴，建立空间直角坐标系O-xyz,则O1（0，1，），A（
，0，0），A1（
，1，
），B（0，2，0），
=（-
，1，-
），
=（
，-1，-
）.
设A1B与AO1所成的角为α，则
cosα=
.
故异面直线A1B与AO1所成角大小为arccos
.
练习册系列答案
相关题目
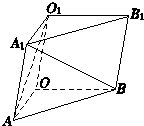如图所示，三棱柱OAB-O1A1B1中，平面OBB1O1⊥平面OAB，∠O1OB=60°，∠AOB=90°，且OB=OO1=2，OA=
斜三棱柱OAB-CA1B1，其中向量
（2002•上海）如图，三棱柱OAB-O1A1B1，平面OBB1O1⊥平面OAB，∠O1OB=60°，∠AOB=90°，且OB=OO1=2，OA=
（2009•闵行区一模）如图，直三棱柱OAB-O1A1B1中，∠AOB=90°，AA1=2，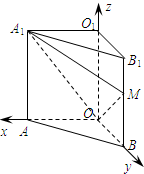
（2009•闵行区一模）如图，直三棱柱OAB-O1A1B1中，∠AOB=90°，M是侧棱BB1上一点，向量