题目内容

斜三棱柱OAB-CA1B1，其中向量
OA
=
a
，
OB
=
b
，
OC
=
.
c
，三个向量之间的夹角均为
π
3
，点M，N分别在CA1，BA1上且
CM
=
1
2
MA1
，
BN
=
NA1
，|
OA
|=2，|
OB
|=2，
|OC|
=4，如图
（1）把向量
AM
用向量
a
，
c
表示出来，并求|
AM
|；
（2）把向量
ON
用
a
，
b
，
c
表示；
（3）求AM与ON所成角的余弦值．
分析：（1）先用
a
、
c
表示
OM
，
AM
，利用
AM
=
OM
-
OA
表示出
AM
，根据向量的模计算公式计算求得|
AM
|．
（2）由
BN
=
NA1
得N为BA1的中点，利用
ON
=
1
2
（
OB
+
OA1
）表示出
ON
．
（3）利用模计算公式求出|
ON
|，利用向量的数量积运算求出
AM
•
ON
，根据cos＜
AM
，
ON
＞=
AM
•
ON
|
AM
||
ON
|
求异面直线所成角的余弦值．
解答：解：（1）如图：
OM
=
OC
+
CM
=
c
+
1
3
a
，
AM
=
OM
-
OA
=
c
+
1
3
a
-
a
=
c
-
2
3
a
，
∵∠AOC=
π
3
，∴|
AM
|=
c
2+
4
9
a
2-2×
2
3
a
•
c
=
16+
16
9
-
4
3
×2×4×
1
2
=
4
7
3
；
（2）∵
OA1
=
OA
+
OC
=
c
+
a
，
OB
=
b
，
又
BN
=
NA1
，N为BA1的中点，
∴
ON
=
1
2
（
OB
+
OA1
）=
1
2
（
a
+
b
+
c
）；
（3）三个向量之间的夹角均是
π
3
，|
ON
|=
1
2
×
4+4+16+2×2×2×
1
2
+2×2×4×
1
2
+2×4×2×
1
2
=
1
2
×
44
=
11
，
∴
AM
•
ON
=(-
2
3
a
+
c
)•
1
2
(
a
+
b
+
c
)=-
1
3
×（4+2×2×
1
2
+2×4×
1
2
）+
1
2
×（2×4×
1
2
+2×4×
1
2
+4×4）=
26
3
，
COS＜
AM
，
ON
＞=
AM
•
ON
|
AM
|•
|ON|
=
26
3
4
7
3
×
11
=
13
77
154
，
故异面直线AM与ON所成的角的余弦值为
13
77
154
．
点评：本题考查了用向量运算求异面直线所成的角，考查了向量的加、减、数量积运算，考查了向量的模运算公式，运算量大，计算时一定要细心．
练习册系列答案
相关题目
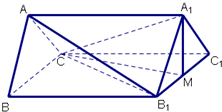精英家教网已知斜三棱柱ABC-A1B1C1的侧面BB1C1C与底面ABC垂直，BB1=BC，∠B1BC=60°，AB=AC，M是B1C1的中点，
（1）求证：AB1∥平面A1CM；
（2）若AB1与平面BB1C1C所成的角为450，求二面角B-AC-B1的余弦值．
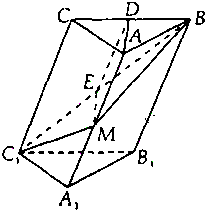在斜三棱柱A1B1C1-ABC中，底面是等腰三角形，AB=AC，侧面BB1C1C⊥底面ABC．
（1）若D是BC的中点，求证：AD⊥CC1；
（2）过侧面BB1C1C的对角线BC1的平面交侧棱于M，若AM=MA1，求证：截面MBC1⊥侧面BB1C1C．
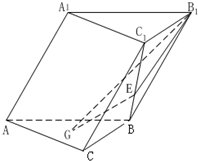如图，在斜三棱柱ABC-A1B1C1　　中，侧面AA1B1B⊥底面ABC，侧棱AA1与底面ABC成600的角，AA1=2．底面ABC是边长为2的正三角形，其重心为G点．E是线段BC1上一点，且BE=
13
BC1．
（1）求证：GE∥侧面AA1B1B；
（2）求平面B1GE与底面ABC所成锐二面角的大小．
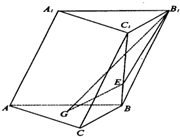精英家教网如图，在斜三棱柱ABC-A1B1C1中，侧面AA1B1B⊥底面ABC，侧棱AA1与底面ABC成60°的角，AA1=2．底面ABC是边长为2的正三角形，其重心为G点，E是线段BC1上一点，且BE=
13
BC1．
（1）求证：GE∥侧面AA1BB；
（2）求平面B1GE与底面ABC所成锐二面角的正切值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网