题目内容
已知函数 ,其中
,其中 .
.
(Ⅰ)若 ,求
,求 的值,并求此时曲线
的值,并求此时曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)求函数 在区间
在区间 上的最小值.
上的最小值.
解:(Ⅰ)已知函数 ,
,
所以 ,
, ,
,
又 ,所以
,所以 .
.
又 ,
,
所以曲线 在点
在点 处的切线方程为
处的切线方程为 .
.
(Ⅱ) ,
,
令 ,则
,则 .
.
(1)当 时,
时, 在
在 上恒成立,所以函数
上恒成立,所以函数 在区间
在区间 上单调递增,所以
上单调递增,所以 ;
;
(2)当 时,在区间
时,在区间 上,
上, ,在区间
,在区间 上,
上, ,所以函数
,所以函数 在区间
在区间 上单调递减,在区间
上单调递减,在区间 上单调递增,且
上单调递增,且 是
是
上唯一极值点,所以 ;
;
(3)当 时,在区间
时,在区间 上,
上, (仅有当
(仅有当 时
时 ),所以
),所以 在区间
在区间 上单调递减
上单调递减
所以函数 .
.
综上所述,当 时,函数
时,函数 的最小值为
的最小值为 ,
,
 时,函数
时,函数 的最小值为
的最小值为

练习册系列答案
相关题目
 左焦点
左焦点 ,倾斜角为
,倾斜角为 的直线交双曲线右支于点
的直线交双曲线右支于点 ,若线段
,若线段 的中点在
的中点在 轴上,则此双曲线的离心率为( )
轴上,则此双曲线的离心率为( ) B.
B.  C.
C. 3 D.
3 D. 
 ,且
,且 ,则
,则 等于
等于  B.
B.  C.
C.  D.
D. 
 中,
中,  ,
, ,则
,则 ;
; 的最小值是 .
的最小值是 .
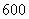 吨,每次都购买
吨,每次都购买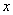 吨(
吨(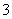 万元/次,
万元/次,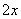 万元.若要使一年的总运费与总存储费用之和最小,则每次需购买 吨.
万元.若要使一年的总运费与总存储费用之和最小,则每次需购买 吨.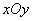 中,已知两定点
中,已知两定点 ,
, .动点
.动点 满足
满足 则点
则点 构成的区域的面积是______;点
构成的区域的面积是______;点 构成的区域的面积是______.
构成的区域的面积是______.