题目内容
已知△ABC的顶点是A(-3,0)、B(2,1)、C(-2,3).求:(1)BC边上的高所在的直线的方程;(2)以线段AB为直径的圆的方程.
【答案】分析:(1)根据B与C的坐标求出直线BC的斜率,根据两直线垂直时斜率乘积为-1,求出BC边上的高所在直线的斜率,然后由A的坐标和求出的斜率写出高所在直线的方程即可;
(2)由点A和点B的坐标,利用中点坐标公式求出线段AB的中点的坐标,因为线段AB为所求圆的直径,所以求出的中点的坐标即为圆心坐标,然后由圆心的坐标和点A的坐标,利用两点间的距离公式求出圆的半径,根据圆心和半径写出圆的标准方程即可.
解答:解:(1)因为直线BC经过B(2,1)和C(-2,3)两点,
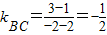 ,
,
∴BC边上的高所在直线的斜率 k=2,
∴BC边上的高所在直线的方程为:y-0=2(x+3),
即2x-y+6=0.
(2)由中点坐标公式得线段AB的中点坐标为E(- ,
, ),即圆心的坐标;
),即圆心的坐标;
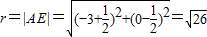 ,
,
故所求圆的方程为:(x+ )2+(y-
)2+(y- )2=
)2=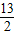 .
.
点评:考查学生会根据一点和斜率或两点坐标写出直线的方程,会利用中点坐标公式求线段的中点坐标,会根据圆心和半径写出圆的标准方程,是一道基础题.
(2)由点A和点B的坐标,利用中点坐标公式求出线段AB的中点的坐标,因为线段AB为所求圆的直径,所以求出的中点的坐标即为圆心坐标,然后由圆心的坐标和点A的坐标,利用两点间的距离公式求出圆的半径,根据圆心和半径写出圆的标准方程即可.
解答:解:(1)因为直线BC经过B(2,1)和C(-2,3)两点,
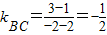 ,
,∴BC边上的高所在直线的斜率 k=2,
∴BC边上的高所在直线的方程为:y-0=2(x+3),
即2x-y+6=0.
(2)由中点坐标公式得线段AB的中点坐标为E(-
 ,
, ),即圆心的坐标;
),即圆心的坐标;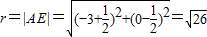 ,
,故所求圆的方程为:(x+
 )2+(y-
)2+(y- )2=
)2=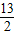 .
.点评:考查学生会根据一点和斜率或两点坐标写出直线的方程,会利用中点坐标公式求线段的中点坐标,会根据圆心和半径写出圆的标准方程,是一道基础题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目