题目内容
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,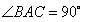 ,A1A⊥平面
,A1A⊥平面
ABC, ,
, ,AC=2,
,AC=2, ,
,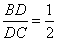 。
。
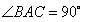 ,A1A⊥平面
,A1A⊥平面ABC,
 ,
, ,AC=2,
,AC=2, ,
,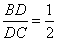 。
。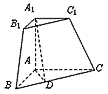
(Ⅰ)证明:平面A1AD⊥平面BCC1B1;
(Ⅱ)求AA1与平面BCC1B1所成角的正弦值。
(Ⅱ)求AA1与平面BCC1B1所成角的正弦值。
| 解:(Ⅰ)如图,建立空间直角坐标系, 则  , ,∵BD:DC=1:2, ∴  , ,∴D点的坐标为  , ,∴  , , , , , , , , , ,∴  , , , ,又  , ,∴BC⊥平面  , ,又  平面 平面 , ,∴平面  平面 平面 。 。 (Ⅱ)设平面  的法向量为 的法向量为 ,则 ,则 , ,即  , ,取  ,得 ,得 , ,∴  , ,因此,AA1与平面BCC1B1所成角的正弦值为  。 。 |
 |

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,

 三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC, ,
, ,AC=2,A1C1=1,
,AC=2,A1C1=1, .
.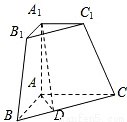 三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC, ,
, ,AC=2,A1C1=1,
,AC=2,A1C1=1, .
.