题目内容

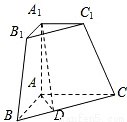
三棱锥被平行于底面ABC的平面所截得的几何体如图所示，截面为A1B1C1，∠BAC=90°，A1A⊥平面ABC，A1A=
3
，AB=
2
，AC=2，A1C1=1，
BD
DC
=
1
2
．
（Ⅰ）证明：平面A1AD⊥平面BCC1B1；
（Ⅱ）求二面角A-CC1-B的大小．
精英家教网

精英家教网
证明：（Ⅰ）∵A1A⊥平面ABC，BC?平面ABC，
∴A1A⊥BC．在Rt△ABC中，AB=
2
，AC=2，∴BC=
6
，
∵BD：DC=1：2，∴BD=
6
3
，又
BD
AB
=
3
3
=
AB
BC
，
∴△DBA∽△ABC，∴∠ADB=∠BAC=90°，即AD⊥BC．
又A1A∩AD=A，∴BC⊥平面A1AD，∵BC?平面BCC1B1，∴平面A1AD⊥平面BCC1B1．

（Ⅱ）如图，作AE⊥C1C交C1C于E点，连接BE，
由已知得AB⊥平面ACC1A1．∴AE是BE在面ACC1A1内的射影．
由三垂线定理知BE⊥CC1，∴∠AEB为二面角A-CC1-B的平面角．
过C1作C1F⊥AC交AC于F点，
则CF=AC-AF=1，C1F=A1A=
3
，∴∠C1CF=60°．
在Rt△AEC中，AE=ACsin60°=2×
3
2
=
3
．
在Rt△BAE中，tanAEB=
AB
AE
=
2
3
=
6
3
．∴∠AEB=arctan
6
3
，
即二面角A-CC1-B为arctan
6
3
．
练习册系列答案
相关题目
精英家教网三棱锥被平行于底面ABC的平面所截得的几何体如图所示，截面为A1B1C1，∠BAC=90°，A1A⊥平面ABC，A1A=
3
，AB=
2
，AC=2，A1C1=1，
BD
DC
=
1
2
．
（Ⅰ）证明：平面A1AD⊥平面BCC1B1；
（Ⅱ）求二面角A-CC1-B的大小．

三棱锥被平行于底面ABC的平面所截得的几何体如图所示，截面为A1B1C1，

∠BAC=90°,A1A⊥平面ABC,A1A=,AB=,AC=2,A1C1=1,=.

(1)证明:平面A1AD⊥平面BCC1B1；

(2)求二面角A—CC1—B的余弦值.
三棱锥被平行于底面ABC的平面所截得的几何体如图所示，截面为A1B1C1，∠BAC=90°，A1A⊥平面ABC，，，AC=2，A1C1=1，．
（Ⅰ）证明：平面A1AD⊥平面BCC1B1；
（Ⅱ）求二面角A-CC1-B的大小．
三棱锥被平行于底面ABC的平面所截得的几何体如图所示，截面为A1B1C1，∠BAC=90°，A1A⊥平面ABC，，，AC=2，A1C1=1，．
（Ⅰ）证明：平面A1AD⊥平面BCC1B1；
（Ⅱ）求二面角A-CC1-B的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网