题目内容
已知二次函数 ,满足:对任意实数
,满足:对任意实数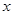 ,都有
,都有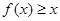 ,且当
,且当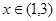 时,有
时,有 成立,又
成立,又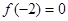 ,则
,则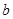 为( )
为( )
A.1 B.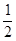 C.2 D.0
C.2 D.0
【答案】
B.
【解析】
试题分析:由条件对任意实数x,都有f(x)≥x,知f(2)≥2成立
∵当x∈(1,3)时,有 成立,
成立,
∴取x=2时, 成立,
成立,
∴f(2)=2.
∴4a+2b+c=2①
∵f(-2)=0
∴4a-2b+c=0②
由①②可得,∴4a+c=2b=1,
∴b= ,故选B.
,故选B.
考点:本题主要考查二次函数性质,方程组解法。
点评:典型题,对恒成立问题,可以任取自变量的值,式子均成立。本题紧紧围绕已知条件,通过 , f(2)=2得到方程组。
, f(2)=2得到方程组。

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
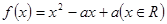 同时满足:①不等式
同时满足:①不等式 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在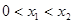 ,使得不等式
,使得不等式 成立.
成立.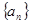 的前
的前 项和
项和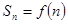 ,
,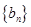 中,令
中,令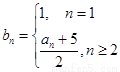 ,
,
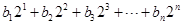 ,求
,求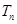 ;
; 中,所有满足
中,所有满足 的正整数
的正整数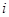 的个数称为这个数列
的个数称为这个数列 (
(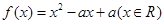 同时满足:
同时满足: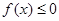 的解集有且只有一个元素;
的解集有且只有一个元素;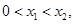 使得不等式
使得不等式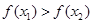 成立.
成立.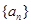 的前
的前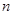 项和
项和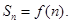
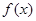 表达式;
表达式;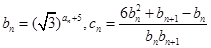 ,
,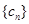 的前
的前 ,
,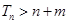 对
对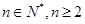
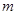 的取值范围.
的取值范围.