题目内容
已知函数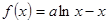 .
.
(1)当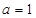 时,求
时,求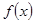 的极值;
的极值;
(2)若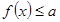 对
对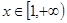 恒成立,求实数
恒成立,求实数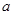 的取值范围.
的取值范围.
(1)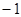 (2)
(2) 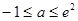
解析试题分析:
(1)确定定义域,保证函数有意义;求导函数,令其等于0,得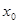 ,判断其单调性,从而确定其极值.
,判断其单调性,从而确定其极值.
(2)根据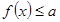 对
对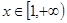 恒成立,可知函数
恒成立,可知函数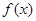 在
在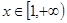 上的最大值小于等于
上的最大值小于等于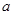 恒成立.利用导数, 通过讨论
恒成立.利用导数, 通过讨论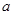 的范围,判断函数的单调性,从而找到函数的最值,最终确定
的范围,判断函数的单调性,从而找到函数的最值,最终确定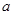 的范围.
的范围.
(1)函数的定义域为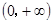 ,由
,由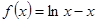 ,知
,知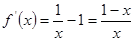 .
.
令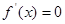 ,得
,得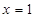 .显然
.显然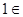
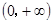 .
.
当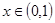 时,
时,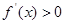
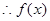 是增函数;
是增函数;
当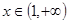 时,
时,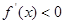
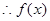 是减函数.
是减函数.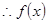 的极大值
的极大值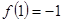 .
.
(2)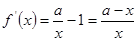 ,
,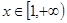
①当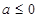 时,
时,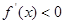
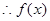 是减函数,即
是减函数,即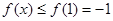
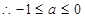 ;
;
②当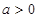 时,当
时,当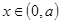 时,
时,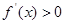
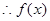 是增函数;
是增函数;
当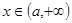 时,
时,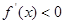
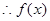 是减函数.
是减函数.
(ⅰ)当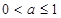 时, 在
时, 在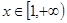 时
时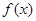 是减函数,即
是减函数,即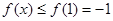
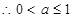 ;
;
(ⅱ) 当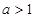 时,当
时,当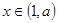 时,
时,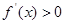
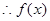 是增函数;当
是增函数;当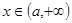 时,
时,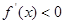
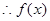 是减函数.
是减函数.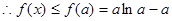 即
即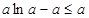
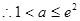 .综上
.综上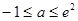 .
.
考点:导数法求极值,分类讨论最值.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
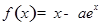
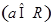 ,
,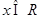 .已知函数
.已知函数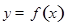 有两个零点
有两个零点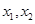 ,且
,且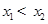 .
. 的取值范围;
的取值范围;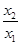 随着
随着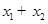 随着
随着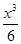 (m为实数).
(m为实数).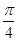 ),f(
),f( 平行直线
平行直线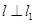 , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程.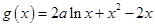 .
.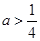 时,讨论函数
时,讨论函数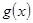 的单调性;
的单调性;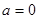 时,在函数
时,在函数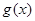 图象上取不同两点A、B,设线段AB的中点为
图象上取不同两点A、B,设线段AB的中点为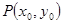 ,试探究函数
,试探究函数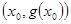 点处的切线与直线AB的位置关系?
点处的切线与直线AB的位置关系?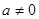 时
时 ,e])都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.
,e])都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.
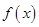 的最大值;
的最大值;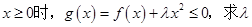 的取值范围.
的取值范围.