题目内容
18.已知平面直角坐标系xOy中,过点P(-1,-2)的直线l的参数方程为$\left\{\begin{array}{l}{x=-1+tcos45°}\\{y=-2+tsin45°}\end{array}\right.$(t为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ•sinθ•tanθ=2a(a>0),直线l与曲线C相交于不同的两点M、N.(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)若|PM|=|MN|,求实数a的值.
分析 (1)利用同角的平方关系以及极坐标方程和直角坐标的互化公式求解;
(2)结合直线的参数方程中参数的几何意义和二次方程的韦达定理,求解即可.
解答 解:(1)∵直线l的参数方程为$\left\{\begin{array}{l}{x=-1+tcos45°}\\{y=-2+tsin45°}\end{array}\right.$(t为参数),
∴直线l的普通方程:x-y-1=0,
∵曲线C的极坐标方程为 ρsinθtanθ=2a(a>0),
∴ρ2sin2θ=2aρcosθ(a>0),
∴曲线C的普通方程:y2=2ax;
(2)∵y2=2ax;
∴x≥0,
设直线l上点M、N对应的参数分别为t1,t2,(t1>0,t2>0),
则|PM|=t1,|PN|=t2,
∵|PM|=|MN|,
∴|PM|=$\frac{1}{2}$|PN|,
∴t2=2t1,
将$\left\{\begin{array}{l}{x=-1+tcos45°}\\{y=-2+tsin45°}\end{array}\right.$(t为参数),代入y2=2ax得
t2-2$\sqrt{2}$(a+2)t+4(a+2)=0,
∴t1+t2=2$\sqrt{2}$(a+2),
t1t2=4(a+2),
∵t2=2t1,
∴a=$\frac{1}{4}$.
点评 本题重点考查了曲线的参数方程和普通方程的互化、极坐标方程和直角坐标方程的互化等知识.

练习册系列答案
相关题目
9.已知直线y=mx与x2+y2-4x+2=0相切,则m值为( )
| A. | ±$\sqrt{3}$ | B. | ±$\frac{\sqrt{3}}{3}$ | C. | ±$\frac{\sqrt{3}}{2}$ | D. | ±1 |
2.若点P是△ABC的外心,且$\overrightarrow{PA}$+$\overrightarrow{PB}$+λ$\overrightarrow{PC}$=$\overrightarrow{0}$,∠C=120°,则实数λ的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -1 | D. | 1 |
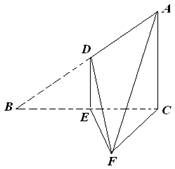 如图,直角△ABC中,∠ACB=90°,BC=2AC=4,D、E分别是AB、BC边的中点,沿DE将△BDE折起至△FDE,且∠CEF=60°.
如图,直角△ABC中,∠ACB=90°,BC=2AC=4,D、E分别是AB、BC边的中点,沿DE将△BDE折起至△FDE,且∠CEF=60°.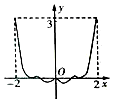



 且
且 ,则当
,则当 时,
时, 的导函数
的导函数 的极小值为 .
的极小值为 .