题目内容
6.函数f(x)=x2-sin|x|在[-2,2]上的图象大致为( )| A. | 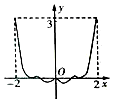 | B. |  | C. |  | D. |  |
分析 求出函数f(x)=x2-sinx在(0,2]上导函数,求出极值点的个数,以及f(2)的值,即可判断函数的图象.
解答 解:函数f(x)=x2-sin|x|在[-2,2]是偶函数,
则:f(x)=x2-sinx在(0,2]可得f′(x)=2x-cosx,令2x-cosx=0,可得方程只有一个解,如图:
可知f(x)=x2-sinx在(0,2]由一个极值点,排除A,C,
f(2)=4-sin2>3,排除D.
故选:B.
点评 本题考查函数的图象的判断,函数的极值的求法,考查转化思想以及计算能力.

练习册系列答案
相关题目
19.F1、F2是双曲线C的焦点,过F1且与双曲线实轴垂直的直线与双曲线相交于A、B,且△F2AB为正三角形,则双曲线的离心率e=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
19.已知$\overrightarrow{m}$,$\overrightarrow{n}$为两个非零向量,且|$\overrightarrow{m}$|=2,|$\overrightarrow{m}$+2$\overrightarrow{n}$|=2,则|$\overrightarrow{n}$|+|2$\overrightarrow{m}$+$\overrightarrow{n}$|的最大值为( )
| A. | 4$\sqrt{2}$ | B. | 3$\sqrt{3}$ | C. | $\frac{7\sqrt{3}}{2}$ | D. | $\frac{8\sqrt{3}}{3}$ |
14.已知函数f(x)=lnx+$\frac{ax}{x+1}$(a∈R).
(1)若函数f(x)在区间(1,4)上单调递增,求a的取值范围;
(2)若函数y=f(x)的图象与直线y=2x相切,求a的值.
(1)若函数f(x)在区间(1,4)上单调递增,求a的取值范围;
(2)若函数y=f(x)的图象与直线y=2x相切,求a的值.
1.设p:2x<1,q:x(x+1)<0,则p是q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.已知双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),过左焦点F1作斜率为$\frac{\sqrt{3}}{3}$的直线交双曲线的右支于点P,且y轴平分线段F1P,则双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$+1 | C. | $\sqrt{2}$ | D. | 2+$\sqrt{3}$ |
15.半径为2的圆C的圆心在第四象限,且与直线x=0和$x+y=2\sqrt{2}$均相切,则该圆的标准方程为( )
| A. | (x-1)2+(y+2)2=4 | B. | (x-2)2+(y+2)2=2 | C. | (x-2)2+(y+2)2=4 | D. | (x-2$\sqrt{2}$)2+(y+2$\sqrt{2}$)2=4 |