题目内容
设△ABC的∠A,∠B,∠C所对的边分别是a,b,c若
=(a,c),
=(cosC,
)且
•
=b.
(1)求角A的大小;
(2)求函数f(x)=2sinxsinAcosx+2cos2 xsinA-sinA在区间[0,
]上的取值范围.
| m |
| n |
| 1 |
| 2 |
| m |
| n |
(1)求角A的大小;
(2)求函数f(x)=2sinxsinAcosx+2cos2 xsinA-sinA在区间[0,
| π |
| 4 |
分析:(1)△ABC中,由
•
=b 可得 a•cosC+
=b,再由正弦定理可得
=cosAsinC,求出 cosA=
,可得A的值.
(2)利用三角函数的恒等变换化简函数f(x)的解析式为
sin(2x+
),由x的范围求出2x+
的范围,从而求得函数f(x)的范围.
| m |
| n |
| c |
| 2 |
| sinC |
| 2 |
| 1 |
| 2 |
(2)利用三角函数的恒等变换化简函数f(x)的解析式为
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
解答:解:(1)△ABC中,由
•
=b 可得 a•cosC+
=b,
∴sinAcosC+
=sinB=sin(A+C),
∴
=cosAsinC,
∴cosA=
,
∴A=
.
(2)函数f(x)=2sinxsinAcosx+2cos2 xsinA-sinA=
sin2x+
cos2 x-
=
sin2x+
cos2x=
sin(2x+
).
∵0≤x≤
,∴
≤2x+
≤
,
∴当 2x+
=
时,函数取得最大值为
,当 2x+
=
时,函数取得最小值为
,
故函数在区间[0,
]上的取值范围是[
,
].
| m |
| n |
| c |
| 2 |
∴sinAcosC+
| sinC |
| 2 |
∴
| sinC |
| 2 |
∴cosA=
| 1 |
| 2 |
∴A=
| π |
| 3 |
(2)函数f(x)=2sinxsinAcosx+2cos2 xsinA-sinA=
| ||
| 2 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| π |
| 4 |
∵0≤x≤
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴当 2x+
| π |
| 4 |
| π |
| 2 |
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
故函数在区间[0,
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
点评:本题主要考查两个向量的数量积公式,三角函数的恒等变换及化简求值,根据三角函数的值求角,求三角函数的值域,属于中档题.

练习册系列答案
相关题目
 =(a,c),
=(a,c), =(cosC,
=(cosC, )且
)且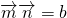 .
. ]上的取值范围.
]上的取值范围.