题目内容
(本小题满分16分)如图,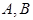 是椭圆
是椭圆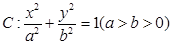 的左、右顶点,椭圆
的左、右顶点,椭圆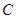 的离心率为
的离心率为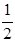 ,右准线
,右准线 的方程为
的方程为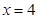 .
.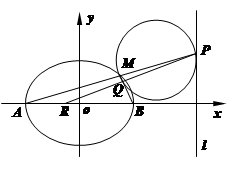
(1)求椭圆方程;
(2)设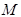 是椭圆
是椭圆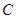 上异于
上异于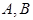 的一点,直线
的一点,直线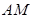 交
交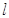 于点
于点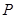 ,以
,以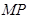 为直径的圆记为
为直径的圆记为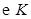 .
.
①若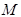 恰好是椭圆
恰好是椭圆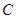 的上顶点,求
的上顶点,求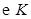 截直线
截直线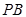 所得的弦长;
所得的弦长;
②设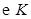 与直线
与直线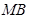 交于点
交于点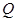 ,试证明:直线
,试证明:直线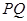 与
与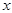 轴的交点
轴的交点 为定点,并求该定点的坐标.
为定点,并求该定点的坐标.
(1) 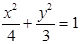 (2) ①
(2) ①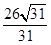 ②见解析
②见解析
解析试题分析:(1)由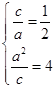 ,解得
,解得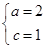 ,故所求椭圆的方程为
,故所求椭圆的方程为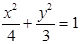 …………………4分
…………………4分
(2)①因为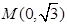 ,所以直线
,所以直线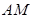 的方程为
的方程为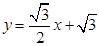 ,则点P的坐标为
,则点P的坐标为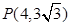 ,
,
从而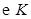 的方程为
的方程为 ,即其圆心为
,即其圆心为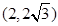 ,半径为
,半径为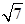 ………… 6分
………… 6分
又直线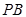 的方程为
的方程为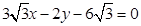 ,故圆心到直线
,故圆心到直线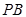 的距离为
的距离为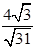 ………8分
………8分
从而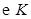 截直线
截直线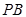 所得的弦长为
所得的弦长为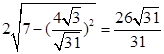 ……………10分
……………10分
②证:设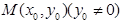 ,则直线
,则直线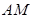 的方程为
的方程为 ,则点P的坐标为
,则点P的坐标为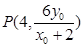 ,
,
又直线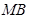 的斜率为
的斜率为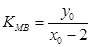 ,而
,而 ,所以
,所以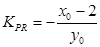 ,
,
从而直线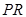 的方程为
的方程为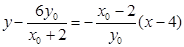 ……………………………13分
……………………………13分
令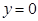 ,得点R的横坐标为
,得点R的横坐标为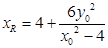 ………………………14分
………………………14分
又点M在椭圆上,所以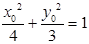 ,即
,即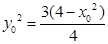 ,故
,故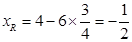 ,
,
所以直线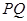 与
与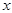 轴的交点
轴的交点 为定点,且该定点的坐标为
为定点,且该定点的坐标为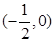 ……………………16分
……………………16分
考点:椭圆性质,直线与圆椭圆的位置关系
点评:本题计算量大,对学生的数据处理能力要求较高

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
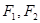 分别为椭圆
分别为椭圆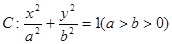 的左、右焦点,点
的左、右焦点,点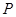 为椭圆上任意一点,
为椭圆上任意一点,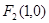 的距离的最大值为
的距离的最大值为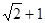 .
.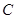 的方程。
的方程。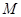 的坐标为
的坐标为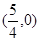 ,过点
,过点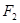 且斜率为
且斜率为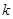 的直线
的直线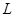 与椭圆
与椭圆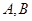 两点。对于任意的
两点。对于任意的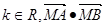 是否为定值?若是求出这个定值;若不是说明理由。
是否为定值?若是求出这个定值;若不是说明理由。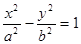 的离心率
的离心率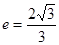 ,过
,过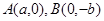 的直线到原点的距离是
的直线到原点的距离是
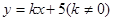 交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.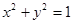 过椭圆
过椭圆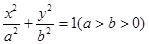 的两焦点,与椭圆有且仅有两个
的两焦点,与椭圆有且仅有两个 与圆
与圆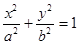 相交于
相交于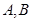 两点记
两点记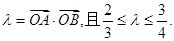
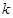 的取值范围;
的取值范围;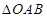 的面积S的取值范围.
的面积S的取值范围.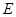 的中心在原点
的中心在原点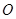 ,焦点
,焦点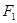 ,
,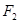 在
在 轴上,经过点
轴上,经过点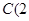 ,
,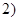 ,且抛物线
,且抛物线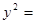
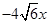 的焦点为
的焦点为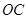 的直线
的直线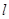 与椭圆
与椭圆 ,
, 两点,当以
两点,当以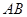 为直径的圆
为直径的圆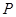 与
与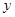 轴相切时,求直线
轴相切时,求直线 是椭圆
是椭圆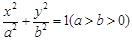 上一点,
上一点, ,
, 是椭圆的两焦点,且满足
是椭圆的两焦点,且满足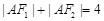
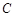 、
、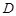 是椭圆上任两点,且直线
是椭圆上任两点,且直线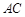 、
、 的斜率分别为
的斜率分别为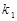 、
、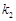 ,若存在常数
,若存在常数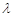 使
使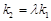 ,求直线
,求直线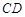 的斜率.
的斜率. 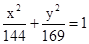 有共同焦点,且过点(0,2)的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率以及渐近线方程.
有共同焦点,且过点(0,2)的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率以及渐近线方程. 轴的负半轴上,过点
轴的负半轴上,过点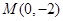 作直线
作直线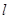 与抛物线交于A,B两点,且满足
与抛物线交于A,B两点,且满足 ,
,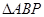 面积的的最大值.
面积的的最大值.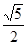 ,且与椭圆
,且与椭圆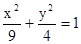 有公共焦点,
有公共焦点,