题目内容
设△ABC的内角A，B，C所对的边分别为a，b，c且cos A＝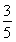
，cos B＝
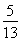，b＝3，则c＝________．
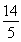
【解析】因为cos A＝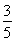
，cos B＝
，所以sin A＝
，
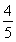sin B＝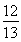
.由正弦定理得
，即
，所以a＝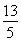
.由余弦定理得b2＝a2＋c2－2accos B，即9＝
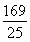＋c2－2c，解得c＝
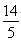(负值舍去)．
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
设△ABC的内角A，B，C所对的边分别为a，b，c且cos A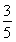＝，cos B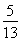＝，b＝3，则c＝________．
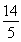
【解析】因为cos A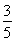＝，cos B＝，所以sin A＝，
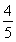sin B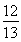＝.由正弦定理得，即，所以a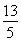＝.由余弦定理得b2＝a2＋c2－2accos B，即9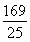＝＋c2－2c，解得c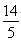＝ (负值舍去)．
阅读快车系列答案
