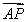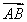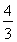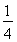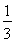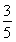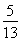题目内容
已知a,b是单位向量,a·b=0,若向量c满足|c-a-b|=1,则|c|的取值范围是( )
A.[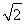 -1,
-1,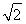 +1] B.[
+1] B.[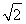 -1,
-1,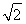 +2]
+2]
C.[1, +1] D.1,
+1] D.1,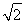 +2
+2
A
【解析】由题可知a·b=0,则a⊥b.又|a|=|b|=1,且|c-a-b|=1,不妨令c=(x,y),a=(1,0),b=(0,1),则(x-1)2+(y-1)2=1.又|c|= ,所以根据几何关系可知|c|max=
,所以根据几何关系可知|c|max= +1=1+
+1=1+ ,|c|min=
,|c|min= -1=
-1= -1,故选A.
-1,故选A.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目