题目内容
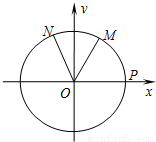
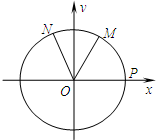 如图,设P是单位圆和x轴正半轴的交点,M、N是单位圆上的两点,O是坐标原点,∠POM=
如图,设P是单位圆和x轴正半轴的交点,M、N是单位圆上的两点,O是坐标原点,∠POM= ,∠PON=α,α∈[0,π)
,∠PON=α,α∈[0,π)
(1)求点M的坐标;
(2)设f(α)= •
• ,求f(α)的取值范围.
,求f(α)的取值范围.
(1)解:设M(x,y),根据三角函数的定义得,
x=cos =
= ,y=sin
,y=sin ,∴M(
,∴M( ).
).
(2)N是单位圆上的点,∠PON=α,α∈[0,π),所以N(cosα,sinα),
∴ ,
, =(cosα,sinα).
=(cosα,sinα).
∴f(α)= •
• =
= =cos(
=cos(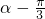 )
)
因为α∈[0,π),∴ ,∴
,∴ <cos(
<cos(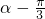 )≤1,
)≤1,
f(α)的取值范围是( ].
].
分析:(1)设出M坐标利用三角函数的定义直接求出M即可.
(2)由题意推出N利用f(α)= •
• ,求出函数的表达式,结合角的范围,求出函数的取值范围.
,求出函数的表达式,结合角的范围,求出函数的取值范围.
点评:本题考查三角函数的定义,向量的数量积,三角函数的化简求值,考查计算能力.
x=cos
 =
= ,y=sin
,y=sin ,∴M(
,∴M( ).
).(2)N是单位圆上的点,∠PON=α,α∈[0,π),所以N(cosα,sinα),
∴
 ,
, =(cosα,sinα).
=(cosα,sinα).∴f(α)=
 •
• =
= =cos(
=cos(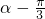 )
)因为α∈[0,π),∴
 ,∴
,∴ <cos(
<cos(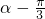 )≤1,
)≤1,f(α)的取值范围是(
 ].
].分析:(1)设出M坐标利用三角函数的定义直接求出M即可.
(2)由题意推出N利用f(α)=
 •
• ,求出函数的表达式,结合角的范围,求出函数的取值范围.
,求出函数的表达式,结合角的范围,求出函数的取值范围.点评:本题考查三角函数的定义,向量的数量积,三角函数的化简求值,考查计算能力.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
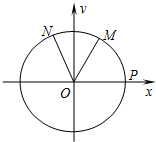 如图,设P是单位圆和x轴正半轴的交点,M、N是单位圆上的两点,O是坐标原点,∠POM=
如图,设P是单位圆和x轴正半轴的交点,M、N是单位圆上的两点,O是坐标原点,∠POM=| π |
| 3 |
| OM |
| ON |
A、(-
| ||||
B、[-
| ||||
C、[-
| ||||
D、(
|
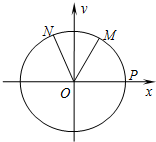 如图,设P是单位圆和x轴正半轴的交点,M、N是单位圆上的两点,O是坐标原点,
如图,设P是单位圆和x轴正半轴的交点,M、N是单位圆上的两点,O是坐标原点,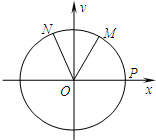 如图,设P是单位圆和x轴正半轴的交点,M、N是单位圆上的两点,O是坐标原点,∠POM=
如图,设P是单位圆和x轴正半轴的交点,M、N是单位圆上的两点,O是坐标原点,∠POM= ,∠PON=α,α∈[0,π],
,∠PON=α,α∈[0,π], ,则f(a)的范围为 .
,则f(a)的范围为 .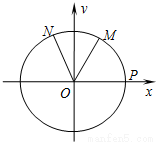
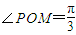 ,∠PON=α,α∈[0,π],
,∠PON=α,α∈[0,π],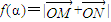 ,则f(a)的范围为 .
,则f(a)的范围为 .