题目内容
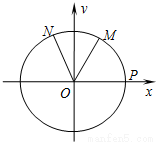
如图,设P是单位圆和x轴正半轴的交点,M、N是单位圆上的两点,O是坐标原点,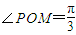 ,∠PON=α,α∈[0,π],
,∠PON=α,α∈[0,π],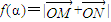 ,则f(a)的范围为 .
,则f(a)的范围为 .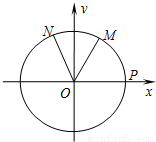
【答案】分析:根据M、N是单位圆上的两点,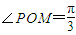 ,∠PON=α,以及三角函数的定义写出点N,M的坐标,求出
,∠PON=α,以及三角函数的定义写出点N,M的坐标,求出 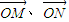 ,并代入
,并代入 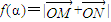 ,利用三角恒等变形,化简为sin(α+
,利用三角恒等变形,化简为sin(α+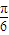 ),要求
),要求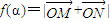 的范围,只需求sin(α+
的范围,只需求sin(α+ ),在区间[0,π]上的最值即可.
),在区间[0,π]上的最值即可.
解答:解:∵M、N是单位圆上的两点,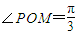 ,∠PON=α,
,∠PON=α,
∴M( ,
,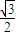 ),N(cosα,sinα),
),N(cosα,sinα),
∴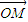 =(
=(  ,
,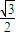 ),
),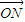 =(cosα,sinα),
=(cosα,sinα),
∴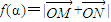 =
=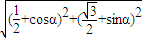 =
=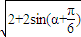
∵α∈[0,π],
∴α+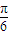 ∈[
∈[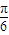 ,
,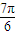 ],
],
∴sin(α+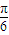 )∈
)∈ .
.
∴f(α)∈[1,2]
故答案为[1,2].
点评:此题是个中档题.考查向量在几何中的应用,同时考查了三角函数的定义和向量的数量积的坐标运算,三角函数在区间上的最值问题,体现了转化的思想,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.
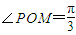 ,∠PON=α,以及三角函数的定义写出点N,M的坐标,求出
,∠PON=α,以及三角函数的定义写出点N,M的坐标,求出 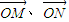 ,并代入
,并代入 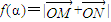 ,利用三角恒等变形,化简为sin(α+
,利用三角恒等变形,化简为sin(α+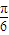 ),要求
),要求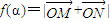 的范围,只需求sin(α+
的范围,只需求sin(α+ ),在区间[0,π]上的最值即可.
),在区间[0,π]上的最值即可.解答:解:∵M、N是单位圆上的两点,
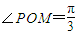 ,∠PON=α,
,∠PON=α,∴M(
 ,
,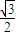 ),N(cosα,sinα),
),N(cosα,sinα),∴
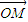 =(
=(  ,
,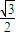 ),
),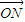 =(cosα,sinα),
=(cosα,sinα),∴
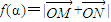 =
=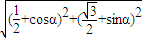 =
=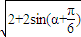
∵α∈[0,π],
∴α+
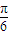 ∈[
∈[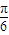 ,
,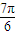 ],
],∴sin(α+
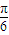 )∈
)∈ .
.∴f(α)∈[1,2]
故答案为[1,2].
点评:此题是个中档题.考查向量在几何中的应用,同时考查了三角函数的定义和向量的数量积的坐标运算,三角函数在区间上的最值问题,体现了转化的思想,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.

练习册系列答案
相关题目
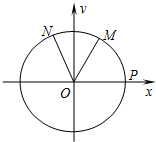 如图,设P是单位圆和x轴正半轴的交点,M、N是单位圆上的两点,O是坐标原点,∠POM=
如图,设P是单位圆和x轴正半轴的交点,M、N是单位圆上的两点,O是坐标原点,∠POM=| π |
| 3 |
| OM |
| ON |
A、(-
| ||||
B、[-
| ||||
C、[-
| ||||
D、(
|
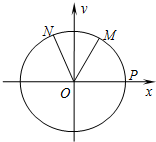 如图,设P是单位圆和x轴正半轴的交点,M、N是单位圆上的两点,O是坐标原点,
如图,设P是单位圆和x轴正半轴的交点,M、N是单位圆上的两点,O是坐标原点,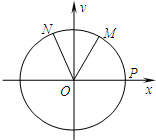 如图,设P是单位圆和x轴正半轴的交点,M、N是单位圆上的两点,O是坐标原点,∠POM=
如图,设P是单位圆和x轴正半轴的交点,M、N是单位圆上的两点,O是坐标原点,∠POM= ,∠PON=α,α∈[0,π],
,∠PON=α,α∈[0,π], ,则f(a)的范围为 .
,则f(a)的范围为 .