题目内容
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)如果对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)是否存在实数![]() ,使得函数
,使得函数![]() 的最大值为0,若存在,求出
的最大值为0,若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
【答案】(1)[0,2];(2)(-∞,![]() );(3)答案见解析.
);(3)答案见解析.
【解析】试题分析:(1)由h(x)=-2(log3x-1)2+2,根据log3x∈[0,2],即可得值域;
(2)由![]() ,令t=log3x,因为x∈[1,9],所以t=log3x∈[0,2],得(3-4t)(3-t)>k对一切t∈[0,2]恒成立,利用二次函数求函数的最小值即可;
,令t=log3x,因为x∈[1,9],所以t=log3x∈[0,2],得(3-4t)(3-t)>k对一切t∈[0,2]恒成立,利用二次函数求函数的最小值即可;
(3)由![]() ,假设最大值为0,因为
,假设最大值为0,因为![]() ,则有
,则有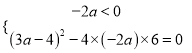 ,求解即可.
,求解即可.
试题解析:
(1)h(x)=(4-2log3x)·log3x=-2(log3x-1)2+2,
因为x∈[1,9],所以log3x∈[0,2],
故函数h(x)的值域为[0,2].
(2)由![]() ,
,
得(3-4log3x)(3-log3x)>k,
令t=log3x,因为x∈[1,9],所以t=log3x∈[0,2],
所以(3-4t)(3-t)>k对一切t∈[0,2]恒成立,
令![]() ,其对称轴为
,其对称轴为![]() ,
,
所以当![]() 时,
时, ![]() 的最小值为
的最小值为![]() ,
,
综上,实数k的取值范围为(-∞,![]() )..
)..
(3)假设存在实数![]() ,使得函数
,使得函数![]() 的最大值为0,
的最大值为0,
由![]() .
.
因为![]() ,则有
,则有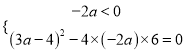 ,解得
,解得![]() ,所以不存在实数
,所以不存在实数![]() ,
,
使得函数![]() 的最大值为0.
的最大值为0.

练习册系列答案
相关题目