题目内容
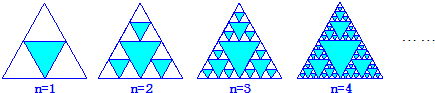
图中的三角形称为谢宾斯基(Sierpinski)三角形.在下图中,将第1个三角形的三边中点为顶点的三角形着色,将第k(k∈N*)个图形中的每个未着色三角形的三边中点为顶点的三角形着色,得到第k+1个图形,这样这些图形中着色三角形的个数依次构成一个数列{an},则数列{an}的通项公式为 .
【答案】分析:由题意可得出此数列是以1为首项,且满足 的数列,由累加法即可求出数列的通项公式
的数列,由累加法即可求出数列的通项公式
解答:解:由题意可得 ,
,
当n≥2时, .
.
故答案为
点评:本题考查归纳推理,考查了识图的能力及归纳推理的能力,解题的关键是得出各个三角形中着色三角形的数量关系即递推关系,本题是归纳考查的常规题,典型题,也是高考的热点题型.
 的数列,由累加法即可求出数列的通项公式
的数列,由累加法即可求出数列的通项公式解答:解:由题意可得
 ,
,当n≥2时,
 .
.故答案为

点评:本题考查归纳推理,考查了识图的能力及归纳推理的能力,解题的关键是得出各个三角形中着色三角形的数量关系即递推关系,本题是归纳考查的常规题,典型题,也是高考的热点题型.

练习册系列答案
相关题目