题目内容
对于函数 ,若在定义域存在实数
,若在定义域存在实数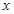 ,满足
,满足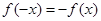 ,则称
,则称 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数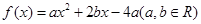 ,试判断
,试判断 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)设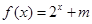 是定义在
是定义在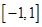 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数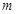 的取值范围.
的取值范围.
(1)是“局部奇函数”;(2) .
.
解析试题分析:(1)本题实质就是解方程 ,如果这个方程有实数解,就说明
,如果这个方程有实数解,就说明 是“局部奇函数”,如果这个方程无实数解,就说明
是“局部奇函数”,如果这个方程无实数解,就说明 不是“局部奇函数”,易知
不是“局部奇函数”,易知 有实数解,因此答案是肯定的;(2)已经明确
有实数解,因此答案是肯定的;(2)已经明确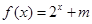 是“局部奇函数”,也就是说方程
是“局部奇函数”,也就是说方程 一定有实数解,问题也就变成方程
一定有实数解,问题也就变成方程 在
在 上有解,求参数
上有解,求参数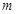 的取值范围,又方程可变形为
的取值范围,又方程可变形为 ,因此求
,因此求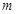 的取值范围,就相当于求函数
的取值范围,就相当于求函数
 的值域,用换元法(设
的值域,用换元法(设 ),再借助于函数
),再借助于函数 的单调性就可求出.
的单调性就可求出.
试题解析:(1) 为“局部奇函数”等价于关于
为“局部奇函数”等价于关于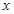 的方程
的方程 有解.
有解.
即
 (3分)
(3分)
有解
 为“局部奇函数”.(5分)
为“局部奇函数”.(5分)
(2)当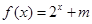 时,
时,  可转化为
可转化为 (8分)
(8分)
因为 的定义域为
的定义域为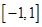 ,所以方程
,所以方程 在
在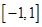 上有解,令
上有解,令 ,(9分)
,(9分)
则
因为 在
在 上递减,在
上递减,在 上递增,
上递增, (11分)
(11分) (12分)
(12分)
即 (14分)
(14分)
考点:新定义概念,方程有解求参数取值范围问题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
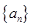 的前
的前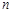 项和
项和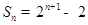 ,数列
,数列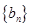 满足
满足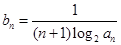 .
.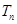 .
.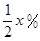 ,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
,该产品每吨的价格上涨百分之几,可使销售的总金额最大?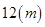 ,高
,高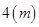 ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大
,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大 米,钢筋网的总长度为
米,钢筋网的总长度为 米.
米.
 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足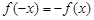 ,则称
,则称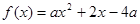
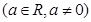 ,试判断
,试判断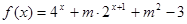 为定义域
为定义域 上的“局部奇函数”,求实数m的取值范围.
上的“局部奇函数”,求实数m的取值范围. 时,该商品的价格上涨多少,才能使销售的总金额达到最大?
时,该商品的价格上涨多少,才能使销售的总金额达到最大?