题目内容
对于函数 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足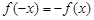 ,则称
,则称 为“局部奇函数”.
为“局部奇函数”.
(1)已知函数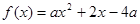
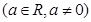 ,试判断
,试判断 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)若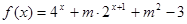 为定义域
为定义域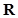 上的“局部奇函数”,求实数m的取值范围.
上的“局部奇函数”,求实数m的取值范围.
(1) 为“局部奇函数”; (2)
为“局部奇函数”; (2)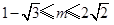
解析试题分析:(1)若方程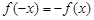 有解,则说明
有解,则说明 是“局部奇函数”,否则,则说明
是“局部奇函数”,否则,则说明 不是“局部奇函数”。 (2)当
不是“局部奇函数”。 (2)当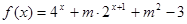 时,
时,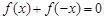 可化为
可化为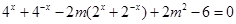 ,用整体思想将
,用整体思想将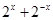 视为整体用
视为整体用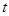 表示。将上式转化为
表示。将上式转化为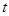 的一元二次函数。根据题意可知此二次函数在其定义域上有解。
的一元二次函数。根据题意可知此二次函数在其定义域上有解。
试题解析:解:(1) 为“局部奇函数”等价于关于x的方程
为“局部奇函数”等价于关于x的方程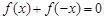 有解.
有解.
当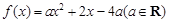 时,
时,
由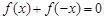 得
得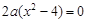
解得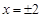 ,
,
所以方程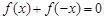 有解,因此
有解,因此 为“局部奇函数”. 4分
为“局部奇函数”. 4分
(2)当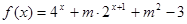 时,
时,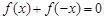 可化为
可化为 .
.
令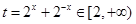 , 则
, 则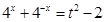 , 6分
, 6分
从而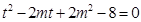 在
在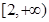 有解即可保证
有解即可保证 为“局部奇函数”. 8分
为“局部奇函数”. 8分
令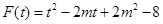 ,
,
1° 当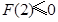 ,
,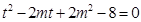 在
在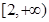 有解,
有解,
由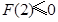 ,即
,即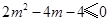 ,解得
,解得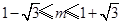 ; 10分
; 10分
2° 当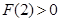 时,
时,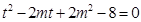 在
在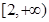 有解等价于
有解等价于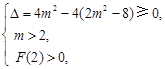 解得
解得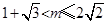 . 13分
. 13分
(说明:也可转化为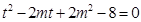 的大根大于等于2求解)
的大根大于等于2求解)
综上,所求实数m的取值范围为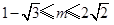 . 14分
. 14分
考点:1新概念问题;2指数函数的值域;3二次函数。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (
(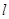 为圆柱的高,
为圆柱的高,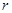 为球的半径,
为球的半径,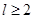 ).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为
).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为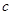 千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为
千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为 千元.
千元.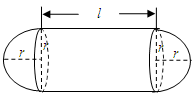
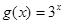 ,
,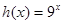 .
.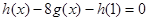 ;
;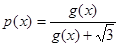 ,求证:
,求证: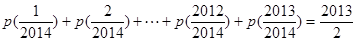 ;
;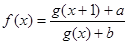 是实数集
是实数集 上的奇函数,且
上的奇函数,且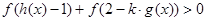 对任意实数
对任意实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,若在定义域存在实数
,若在定义域存在实数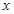 ,满足
,满足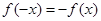 ,则称
,则称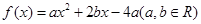 ,试判断
,试判断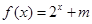 是定义在
是定义在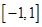 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数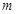 的取值范围.
的取值范围. (万元)与处理量
(万元)与处理量 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: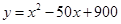 ,且每处理一吨废弃物可得价值为
,且每处理一吨废弃物可得价值为 万元的某种产品,同时获得国家补贴
万元的某种产品,同时获得国家补贴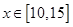 时,判断该项举措能否获利?如果能获利,求出最大利润;
时,判断该项举措能否获利?如果能获利,求出最大利润; .
.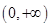 内的任意
内的任意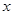 ,总有
,总有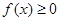 成立,求实数
成立,求实数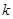 的取值范围;
的取值范围; 在区间
在区间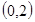 内有两个不同的零点
内有两个不同的零点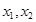 ,求:
,求: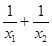 的取值范围.
的取值范围. 及二次函数
及二次函数 满足:
满足: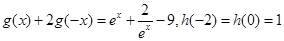 且
且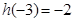 。
。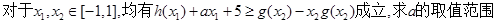 ;
;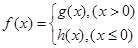 ,讨论方程
,讨论方程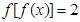 的解的个数情况.
的解的个数情况.