题目内容
已知点A(3,-4)、B(-1,2),点P在直线AB上,且|
|=2|
|,则点P的坐标是
| PA |
| PB |
(
,0)或(-5,8)
| 1 |
| 3 |
(
,0)或(-5,8)
.| 1 |
| 3 |
分析:由题设条件知A,P,B三点共线,且有
=±2
,设出点P的坐标,分两类利用向量相等的条件建立方程求出点P的坐标即可
| PA |
| PB |
解答:解:由题意点A(3,-4)、B(-1,2),点P在直线AB上,且|
|=2|
|,
∴
=±2
令P(x,y),则有
=(3-x,-4-y),
=(-1-x,2-y)
若
=2
,则有
,解得
即P(-5,8)
若
=-2
,则有
,解得
,即P(
,0)
综上知,点P的坐标是(
,0)或(-5,8)
故答案为:(
,0)或(-5,8).
| PA |
| PB |
∴
| PA |
| PB |
令P(x,y),则有
| PA |
| PB |
若
| PA |
| PB |
|
|
若
| PA |
| PB |
|
|
| 1 |
| 3 |
综上知,点P的坐标是(
| 1 |
| 3 |
故答案为:(
| 1 |
| 3 |
点评:本题考查向量共线的坐标表示,向量相等的条件,解题的关键是由题设条件得出两向量的数乘关系,再利用向量相等的条件得到坐标的方程求出点P的坐标,本考点是向量中重要考点,属于向量中框架知识点,在新教材实验区,此考点是每年高考必考考点.

练习册系列答案
相关题目
已知点A(-3,-4),B(6,3)到直线l:ax+y+1=0的距离相等,则实数a的值等于( )
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
已知点A(3,4),B(6,m)到直线3x+4y-7=0的距离相等,则实数m等于( )
A、
| ||||
B、-
| ||||
| C、1 | ||||
D、
|
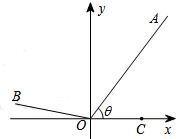 如图,已知点A(3,4),C(2,0),点O为坐标原点,点B在第二象限,且|OB|=3,记∠AOC=θ.高.
如图,已知点A(3,4),C(2,0),点O为坐标原点,点B在第二象限,且|OB|=3,记∠AOC=θ.高.