题目内容
已知点A(3,4),现将射线OA绕坐标原点O顺时针旋转
至OB处,若角α以x轴非负半轴为始边、以射线OB为终边,则tan(
-α)=( )
| π |
| 4 |
| 3π |
| 2 |
分析:由已知,将α进行转化表示,利用两角差的正切公式求正切,再利用诱导公式求解.
解答: 解:如图所示:
解:如图所示:
不妨设α=∠AOx-∠AOB=∠AOx-45°,则tan=∠AOx=
.
则tanα=tan(∠AOx-45°)=
=
=
,
则tan(
-α)=cotα=
=7.
故选:B
 解:如图所示:
解:如图所示:不妨设α=∠AOx-∠AOB=∠AOx-45°,则tan=∠AOx=
| 4 |
| 3 |
则tanα=tan(∠AOx-45°)=
| tan∠AOx-tan45° |
| 1+tan∠AOxtan45° |
| ||
1+
|
| 1 |
| 7 |
则tan(
| 3π |
| 2 |
| 1 |
| tanα |
故选:B
点评:本题考查三角函数式求值,用到的知识点有:任意角三角函数的定义,两角差的正切公式,诱导公式.本题关键是将α进行转化表示.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
已知点A(-3,-4),B(6,3)到直线l:ax+y+1=0的距离相等,则实数a的值等于( )
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
已知点A(3,4),B(6,m)到直线3x+4y-7=0的距离相等,则实数m等于( )
A、
| ||||
B、-
| ||||
| C、1 | ||||
D、
|
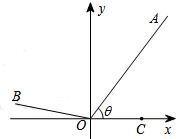 如图,已知点A(3,4),C(2,0),点O为坐标原点,点B在第二象限,且|OB|=3,记∠AOC=θ.高.
如图,已知点A(3,4),C(2,0),点O为坐标原点,点B在第二象限,且|OB|=3,记∠AOC=θ.高.