题目内容
a为何值时,函数f(x)=asinx+
思路分析:x=![]() 处有极值即x=
处有极值即x=![]() 可使f′(x)=0.转化为关于a的方程.从而求得a的值.进而求极值.
可使f′(x)=0.转化为关于a的方程.从而求得a的值.进而求极值.
解:f′(x)=(asinx)′+(![]() sin3x)′=acosx+cos3x.?
sin3x)′=acosx+cos3x.?
令f′(x)=0,
可得:acosx+cos3x=0.
将x=![]() 代入可得a=2.?
代入可得a=2.?
∴f′(x)=2cosx+cos3x?
=cosx(2cosx+1)·(2cosx-1)=0.?
解之:x=kπ+![]() 或x=kπ±
或x=kπ±![]() .?
.?
在x=![]() 附近,当x<
附近,当x<![]() 时,f′(x)>0,?
时,f′(x)>0,?
当x>![]() 时,f′(x)<0.?
时,f′(x)<0.?
∴f(x)在![]() 取极大值,且f(x)极大值=?f(
取极大值,且f(x)极大值=?f(![]() =
=![]() ).
).
温馨提示
判断极值类型是依据在这个x0前后f′(x)的符号;即判断f(x)在x0前后的单调性;先增后减处取极大值,先减后增处取极小值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
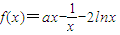 .
.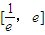 上有零点.
上有零点.