题目内容
2.设F为抛物线x2=4y的焦点,A、B、C为该抛物线上三点,若$\overrightarrow{FA}$+$\overrightarrow{FB}$+$\overrightarrow{FC}$=$\overrightarrow{0}$,则|FA|+|FB|+|FC|的值为( )| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
分析 由题意可得F(0,1)是三角形ABC的重心,故$\frac{{y}_{1}+{y}_{2}+{y}_{3}}{3}$=1,再由抛物线的定义可得|FA|+|FB|+|FC|=(y1+1)+(y2+1)+(y3+1)=6.
解答 解:抛物线x2=4y焦点坐标F(0,1),准线方程:y=-1,
设A(x1,y1),B(x2,y2),C(x3,y3)
∵$\overrightarrow{FA}$+$\overrightarrow{FB}$+$\overrightarrow{FC}$=$\overrightarrow{0}$,
∴点F是△ABC重心,则$\frac{{y}_{1}+{y}_{2}+{y}_{3}}{3}$=1,
∴y1+y2+y3=3.
由抛物线的定义可知:|FA|+|FB|+|FC|=(y1+1)+(y2+1)+(y3+1)=6,
∴|FA|+|FB|+|FC|=6,
故选B.
点评 本题考查三角形的重心坐标公式,抛物线的定义、标准方程,以及简单性质的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.某种产品按质量标准分成五个等级,等级编号依次为1,2,3,4,5.现从一批产品中随机抽取20件,对其等级编号进行统计分析,得到频率分布表如下:
(1)若所抽取的20件产品中,等级编号为4的恰有3件,等级编号为5的恰有2件,求a,b,c的值;
(2)在(1)的条件下,将等级编号为4的3件产品记为x1,x2,x3,等级编号为5的2件产品记为y1,y2,现从x1,x2,x3,y1,y2这5件产品中任取两件(假定每件产品被取出的可能性相同),写出所有可能的结果,并求这两件产品的等级编号恰好相同的概率.
| 等级 | 1 | 2 | 3 | 4 | 5 |
| 频率 | a | 0.2 | 0.45 | b | c |
(2)在(1)的条件下,将等级编号为4的3件产品记为x1,x2,x3,等级编号为5的2件产品记为y1,y2,现从x1,x2,x3,y1,y2这5件产品中任取两件(假定每件产品被取出的可能性相同),写出所有可能的结果,并求这两件产品的等级编号恰好相同的概率.
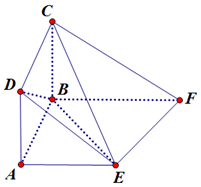 在如图所示的多面体ABCDEF中,四边形ABCD为正方形,底面ABFE为直角梯形,∠ABF为直角,$AE∥BF,AB=\frac{1}{2}BF=1$,
在如图所示的多面体ABCDEF中,四边形ABCD为正方形,底面ABFE为直角梯形,∠ABF为直角,$AE∥BF,AB=\frac{1}{2}BF=1$, 抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的抛物面围成的几何体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是( )
抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的抛物面围成的几何体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是( )