题目内容
某厂生产甲、乙两种产品每吨所需的煤、电和产值如下表所示.
| | 用煤(吨) | 用电(千瓦) | 产值(万元) |
| 甲产品 | 7 | 20 | 8 |
| 乙产品 | 3 | 50 | 12 |
甲产品5吨,乙产品7吨,则该厂日产值最大,最大日产值为124吨
解析试题分析:先由线性约束条件作出可行域,再由目标函数得出最优解.
试题解析:设该厂每天安排生产甲产品x吨,乙产品y吨,则日产值 , (1分)
, (1分)
线性约束条件为 . (3分)
. (3分)
作出可行域. (7分)
把 变形为一组平行直线系
变形为一组平行直线系 ,由图可知,当直线
,由图可知,当直线 经过可行域上的点M时,截距
经过可行域上的点M时,截距 最大,即z取最大值.
最大,即z取最大值.
解方程组 ,得交点
,得交点 , (12分)
, (12分) . (13分)
. (13分)
所以,该厂每天安排生产甲产品5吨,乙产品7吨,则该厂日产值最大,最大日产值为124吨 (14分)
考点:线性规划问题.

练习册系列答案
相关题目
关于x的不等式 的解集中只有一个元素,则实数m =( ).
的解集中只有一个元素,则实数m =( ).
A. | B.2 | C. | D.不存在 |
不等式 的解集为
的解集为 ,那么( )
,那么( )
A. | B. | C. | D. |
设x1和x2是方程x2+px+4=0的两个不相等的实数根,则 ( )
| A.|x1|>2且|x2|>2 | B.|x1+x2|<4 |
| C.|x1+x2|>4 | D.|x1|=4且|x2|=1 |
 ,其中
,其中 .
. 时,证明
时,证明 ;
; 在区间
在区间 ,
,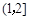 内各有一个根,求
内各有一个根,求 的取值范围;
的取值范围; 的首项
的首项 ,前
,前 项和
项和 ,
, ,求
,求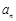 ,并判断
,并判断 的二次函数
的二次函数 .
. 和
和 ,分别从集合P和Q中随机取一个数作为
,分别从集合P和Q中随机取一个数作为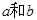 ,求函数
,求函数 在区间
在区间 上是增函数的概率;
上是增函数的概率; 是区域
是区域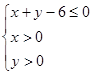 内的随机点,求函数
内的随机点,求函数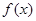 在区间
在区间 满足约束条件
满足约束条件 ,求
,求 的最大值
的最大值 ,则z=3x+2y的最大值是 .
,则z=3x+2y的最大值是 . 表示的平面区域.
表示的平面区域.