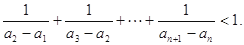题目内容
设等差数列{an}的前n项和为Sn,且S4=4S2,a2n=2an+1.
(1)求数列{an}的通项公式;
(2)设数列{bn}满足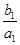 +
+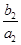 +…+
+…+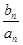 =1-
=1-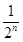 ,n∈N* ,求{bn}的前n项和Tn.
,n∈N* ,求{bn}的前n项和Tn.
(1) an=2n-1,n∈N* (2) Tn=3-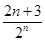
解析解:(1)设等差数列{an}的首项为a1,公差为d.
由S4=4S2,a2n=2an+1得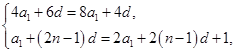
解得a1=1,d=2.
因此an=2n-1,n∈N*.
(2)由已知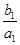 +
+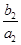 +…+
+…+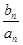 =1-
=1-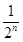 ,n∈N*,
,n∈N*,
当n=1时,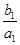 =
= ;
;
当n≥2时,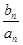 =1-
=1-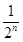 -(1-
-(1- )=
)=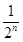 .
.
所以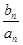 =
=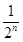 ,n∈N*.
,n∈N*.
由(1)知an=2n-1,n∈N*,
所以bn=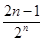 ,n∈N*.
,n∈N*.
又Tn= +
+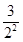 +
+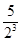 +…+
+…+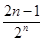 ,
, Tn=
Tn=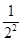 +
+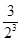 +…+
+…+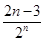 +
+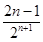 ,
,
两式相减得 Tn=
Tn= +(
+( +
+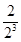 +…+
+…+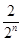 )-
)-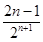
=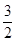 -
-
=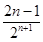 ,
,
所以Tn=3-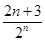 .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
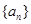 中,已知
中,已知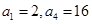 .
.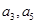 分别为等差数列
分别为等差数列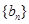 的第3项和第5项,试求数列
的第3项和第5项,试求数列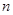 项和
项和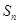 。
。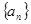
 中,其前
中,其前 项和为
项和为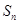 ,满足
,满足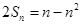 .
. (
(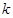 为正整数),求数列
为正整数),求数列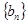 的前
的前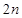 项和
项和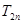 .
.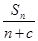 (c≠0)构成的新数列为{bn},求证:当且仅当c=-
(c≠0)构成的新数列为{bn},求证:当且仅当c=-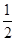 时,数列{bn}是等差数列.
时,数列{bn}是等差数列.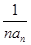 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.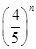 Sn,是否存在正整数m,对一切正整数n,总有Tn≤Tm?若存在,求m的值;若不存在,说明理由.
Sn,是否存在正整数m,对一切正整数n,总有Tn≤Tm?若存在,求m的值;若不存在,说明理由. <2.
<2.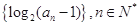 为等差数列,且
为等差数列,且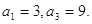
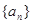 的通项公式;
的通项公式;