题目内容
设α∈R,f(x)=cosx(asinx-cosx)+cos2(| π |
| 2 |
| π |
| 3 |
| π |
| 4 |
| 11π |
| 24 |
分析:利用二倍角公式化简函数f(x),然后f(-
)=f(0),求出a的值,进一步化简为f(x)=2sin(2x-
),然后根据x的范围求出2x-
,的范围,利用单调性求出函数的最大值和最小值.
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
解答:解:f(x)=cosx(asinx-cosx)+cos2(
-x)
=asinxcosx-cos2x+sin2x
=
sin2x-cos2x
由f(-
)=f(0)得-
•
+
=-1
解得a=2
所以f(x)=2sin(2x-
),
所以x∈[
,
]时2x-
∈[
,
],f(x)是增函数,
所以x∈[
,
]时2x-
∈[
,
],f(x)是减函数,
函数f(x)在[
,
]上的最大值是:f(
)=2;
又f(
)=
,f(
)=
;
所以函数f(x)在[
,
]上的最小值为:f(
)=
;
| π |
| 2 |
=asinxcosx-cos2x+sin2x
=
| a |
| 2 |
由f(-
| π |
| 3 |
| ||
| 2 |
| a |
| 2 |
| 1 |
| 2 |
解得a=2
| 3 |
所以f(x)=2sin(2x-
| π |
| 6 |
所以x∈[
| π |
| 4 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 2 |
所以x∈[
| π |
| 3 |
| 11π |
| 24 |
| π |
| 6 |
| π |
| 2 |
| 3π |
| 4 |
函数f(x)在[
| π |
| 4 |
| 11π |
| 24 |
| π |
| 3 |
又f(
| π |
| 4 |
| 3 |
| 11π |
| 24 |
| 2 |
所以函数f(x)在[
| π |
| 4 |
| 11π |
| 24 |
| 11π |
| 24 |
| 2 |
点评:本题是中档题,考查三角函数的化简,二倍角公式的应用,三角函数的求值,函数的单调性、最值,考查计算能力,常考题型.

练习册系列答案
相关题目
 -x)满足
-x)满足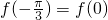 ,求函数f(x)在
,求函数f(x)在 上的最大值和最小值.
上的最大值和最小值. -x)满足
-x)满足 ,求函数f(x)在
,求函数f(x)在 上的最大值和最小值.
上的最大值和最小值.