题目内容
设λ∈R,f(x)=cosx(λsinx-cosx)+cos2(
-x)满足f(-
)=f(0).
(1)求函数f(x)的对称轴和单调递减区间;
(2)设△ABC三内角A,B,C所对边分别为a,b,c且
=-
,求f(x)在(0,A]上的值域.
| π |
| 2 |
| π |
| 3 |
(1)求函数f(x)的对称轴和单调递减区间;
(2)设△ABC三内角A,B,C所对边分别为a,b,c且
| cosA |
| cosB |
| a |
| b+2c |
分析:(1)依题意,f(-
)=f(0)⇒λ=2
,从而可求得f(x)=2sin(2x-
),利用正弦函数的对称轴方程可求得函数f(x)的对称轴,继而可得其单调递减区间;
(2)利用正弦定理,可将条件变形为sin(A+B)=-2cosAsinC,可求得A=
,利用正弦函数的单调性可求得f(x)在(0,A]上的值域.
| π |
| 3 |
| 3 |
| π |
| 6 |
(2)利用正弦定理,可将条件变形为sin(A+B)=-2cosAsinC,可求得A=
| 2π |
| 3 |
解答:解:(1)f(x)=λsinxcosx-cos2x+sin2x
=
λsin2x-cos2x,
∵f(-
)=f(0),
∴λ=2
…3分
∴f(x)=2sin(2x-
),
对称轴为:x=
+
(x∈Z),…5分
∴f(x)=2sin(2x-
)的单调递减区间为[kπ+
,kπ+
](k∈Z)…7分
(2)∵
=-
,由正弦定理,可变形为:sin(A+B)=-2cosAsinC,
∴cosA=-
,
∴A=
------------(10分)
∴x∈(0,
],
∴f(x)∈[-1,2]---------------(14分)
=
| 1 |
| 2 |
∵f(-
| π |
| 3 |
∴λ=2
| 3 |
∴f(x)=2sin(2x-
| π |
| 6 |
对称轴为:x=
| kπ |
| 2 |
| π |
| 3 |
∴f(x)=2sin(2x-
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
(2)∵
| cosA |
| cosB |
| a |
| b+2c |
∴cosA=-
| 1 |
| 2 |
∴A=
| 2π |
| 3 |
∴x∈(0,
| 2π |
| 3 |
∴f(x)∈[-1,2]---------------(14分)
点评:本题考查三角函数中的恒等变换应用,着重考查正弦函数的对称轴方程、单调性及正弦定理,属于中档题.

练习册系列答案
相关题目
 -x)满足
-x)满足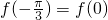 ,求函数f(x)在
,求函数f(x)在 上的最大值和最小值.
上的最大值和最小值. -x)满足
-x)满足 ,求函数f(x)在
,求函数f(x)在 上的最大值和最小值.
上的最大值和最小值.