题目内容
椭圆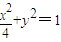
的短轴为B1B2，点M是椭圆上除B1，B2外的任意一点，直线MB1，MB2在x轴上的截距分别为x1，x2，则x1•x2= ．
【答案】分析：解法一：运用特值法，取M为椭圆右顶点（2，0），则x1=2，x2=2，由此可求出x1•x2的值．
解法二：设M（2cosθ，sinθ），直线B1M的方程为：
，令y=0，得
，直线B2M的方程为：
，令y=0，得
，由此可求出x1•x2的值．
解答：解法一：取M为椭圆右顶点（2，0），则x1=2，x2=2，∴x1•x2=4．
解法二：由椭圆
得
，θ为参数，设M（2cosθ，sinθ），
直线B1M的方程为：
，令y=0，得
，
直线B2M的方程为：
，令y=0，得
，
∴x1•x2=
．
答案：4．
点评：特值法是求解选择题和填空题的有效方法．
解法二：设M（2cosθ，sinθ），直线B1M的方程为：
，令y=0，得，直线B2M的方程为：，令y=0，得，由此可求出x1•x2的值．解答：解法一：取M为椭圆右顶点（2，0），则x1=2，x2=2，∴x1•x2=4．
解法二：由椭圆
得，θ为参数，设M（2cosθ，sinθ），直线B1M的方程为：
，令y=0，得，直线B2M的方程为：
，令y=0，得，∴x1•x2=
．答案：4．
点评：特值法是求解选择题和填空题的有效方法．
练习册系列答案
相关题目
椭圆
+y2=1的长轴为A1A2，短轴为B1B2，将坐标平面沿y轴折成一个二面角，使点A1在平面B1A2B2上的射影恰是该椭圆的一个焦点，则此二面角的大小为（ ）
| x2 |
| 4 |
| A、30 | B、45 |
| C、60 | D、arctan2 |
的短轴为B1B2，点M是椭圆上除B1，B2外的任意一点，直线MB1，MB2在x轴上的截距分别为x1，x2，则x1•x2=________．
+
=1的短轴为B1B2，F1为椭圆的一个焦点,则∠B1F1B2的度数为( )